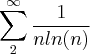
eu sei fazer o teste (é divergente) mas n consigo desenvolver as condições que seriam:
1) ser decrescente (provando pelo teste da derivada primeira
2) ter termos positivos p/
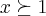 e ser contínua
e ser contínua mas n consigo calcular a derivada primeira (acredito que seja pela regra do quociente)


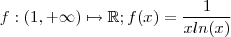 e considere
e considere 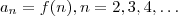 .
. 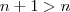 ,então
,então 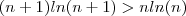 ... ( qualquer função logarítmica é estritamente monótona)
... ( qualquer função logarítmica é estritamente monótona) 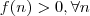 é o suficiente mostrar que
é o suficiente mostrar que 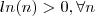 . Para tal , basta usar que
. Para tal , basta usar que  e que qualquer função logarítmica é estritamente monótona .Quanto a continuidade , se
e que qualquer função logarítmica é estritamente monótona .Quanto a continuidade , se 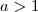 então o limite da função quando
então o limite da função quando  é o próprio valor da função no ponto
é o próprio valor da função no ponto  (Fácil verificar) .
(Fácil verificar) .
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)