Estou tentando resolver este limite por L'Hospital mas nunca consigo eliminar a indeterminação...alguma idéia ???

Se eu derivar seguidas vezes ainda não consigo eliminar a indeterminação





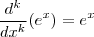 e que
e que 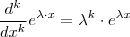 para qualquer natural
para qualquer natural  . Além disso note que
. Além disso note que 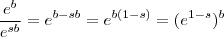 .Tem alguma informação sobre o número
.Tem alguma informação sobre o número  ? Se ele for menor que
? Se ele for menor que  segue que
segue que 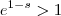 ,caso contrário teremos
,caso contrário teremos 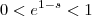 . Para concluir basta responder o que acontece com a função exponencial de base positiva e menor que 1 e com a de base maior que 1 lá no infinito .
. Para concluir basta responder o que acontece com a função exponencial de base positiva e menor que 1 e com a de base maior que 1 lá no infinito .
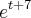
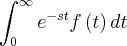


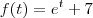 . Temos que
. Temos que  .
. 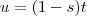 e
e 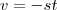 [/tex] as derivadas nos dá respectivamente ,
[/tex] as derivadas nos dá respectivamente ,  e
e  assuma a princípio que
assuma a princípio que  trataremos deste caso depois .Neste caso , teremos
trataremos deste caso depois .Neste caso , teremos 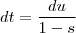 e
e  já que você considerou
já que você considerou 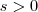 (ou seja ,
(ou seja , )
)  e segundo
e segundo 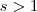 .
.  e
e 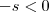 e assim quando
e assim quando  ,
,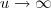 e
e 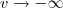 , quando
, quando  teremos também
teremos também  ,renovando os limites de integração , a nova integral se escreve
,renovando os limites de integração , a nova integral se escreve 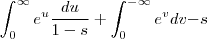 ou ainda
ou ainda  .
.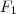 real a qual depende da variável
real a qual depende da variável  que pertence
que pertence  . (Isto se a integral convergir )
. (Isto se a integral convergir ) 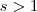 ,então
,então 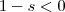 e
e 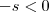 e assim , quando
e assim , quando  teremos que
teremos que 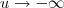 e
e 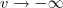 e como já vimos acima quando t =0 , v=u= 0 . Podemos usar a mesma expressão (*) apenas trocando os limites de integração e teremos outra função
e como já vimos acima quando t =0 , v=u= 0 . Podemos usar a mesma expressão (*) apenas trocando os limites de integração e teremos outra função 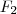 real dependendo da variável
real dependendo da variável  a qual pertence
a qual pertence 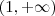 , dada por
, dada por 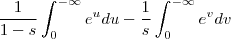 .
. .
.  e esta integral não converge .
e esta integral não converge .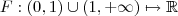 dada por
dada por 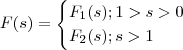 .
.
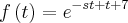
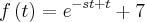

 e não como eu tinha considerado . Neste caso é até mais fácil . Basta ver que
e não como eu tinha considerado . Neste caso é até mais fácil . Basta ver que 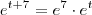 e portanto o integrando se escreve
e portanto o integrando se escreve  .
.  no post acima , e considerar a outra multiplicado por
no post acima , e considerar a outra multiplicado por  .
.  ,
,  e
e 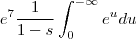 ,
, 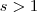 .
.


 será maior que 1 . Por quê a integral
será maior que 1 . Por quê a integral  não converge (1>s>0) , já a outra
não converge (1>s>0) , já a outra 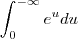 (s>1) converge . Você mesmo notou isto na sua solução pelo que vi . É isso .
(s>1) converge . Você mesmo notou isto na sua solução pelo que vi . É isso .
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.