Danilo escreveu:Encontrar a área da região delimitada pelas curvas dadas.
São elas: x=y²-2, y =1, x=
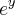
, y =-1.
Eu geralmente consigo calcular, mas neste caso o fato de x estar em função de y, y estar em função de x e de ter 4 gráficos confunde e MUITO a minha cabeça. Eu preciso muito entender isso... Grato!
Não tem mistério. Se você sabe fazer quando temos y = f(x), então é só usar as mesmas ideias para fazer x = f(y).
Vamos começar com a curva:
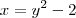
Por um momento, imagine que a curva fosse na verdade o contrário:

O que essa curva representa? Ora, provavelmente você já percebeu que é uma parábola! As características básicas dessa parábola estão abaixo.
(1) Ela corta o eixo x nos pontos:
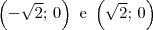
(2) Ela corta o eixo y no ponto:
(0; -2)
Agora vamos voltar a curva original. O que ela representa? Ora, uma parábola também! Só que dessa vez suas caraterísticas básicas são as seguintes.
(1) Ela corta o eixo x no ponto:
(-2; 0)
(2) Ela corta o eixo y nos pontos:
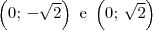
Vamos agora comparar os gráficos dessas curvas.
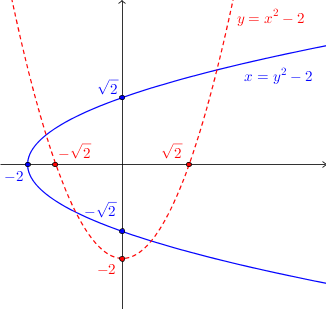
- figura1.png (12.06 KiB) Exibido 3497 vezes
Continuando a resolução do exercício, vamos analisar a curva

Novamente, por um momento, imagine que a curva fosse:
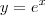
O que ela representa? Você já deve saber que ela representa o gráfico de uma função exponencial. Suas características básicas estão abaixo.
(1) Ela não corta o eixo x (mas fica cada vez mais próximo dele).
(2) Ela corta o eixo y no ponto (0; 1).
Voltando para a curva original, você deve concluir que suas características básicas serão as seguintes.
(1) Ela corta o eixo x no ponto (1; 0).
(2) Ela não corta o eixo y (mas fica cada vez mais próximo dele).
Vamos agora comparar os gráficos dessas curvas.
- figura2.png (5.05 KiB) Exibido 3497 vezes
Falta agora analisar as curvas y = 1 e y = -1. No primeiro caso, temos uma curva formada por todos os pontos do plano que possuem a mesma coordenada y (sendo específico, igual a 1). O que ela representa? Ora, uma reta paralela ao eixo x e cortando o eixo y em (0, 1). Usando uma análise semelhante, você deve concluir que no segundo caso temos uma reta paralela ao eixo x e cortando o eixo y em (0, -1). Vejamos os gráficos dessas curvas.
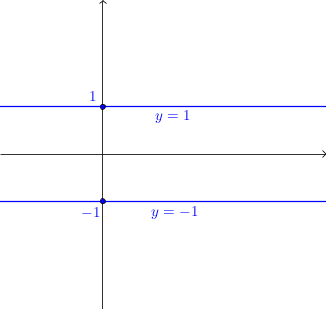
- figura3.png (1.7 KiB) Exibido 3497 vezes
Agora que já conhecemos os gráficos das curvas dadas no exercício, vamos representá-los juntos (e destacar a região delimitada por eles).

- figura4.png (7.55 KiB) Exibido 3497 vezes
Enxergando x como função de y, note que a região delimitada terá área dada por:
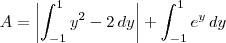
Agora basta resolver as integrais para concluir o exercício. Continue a partir daí.
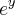 , y =-1.
, y =-1. 
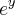 , y =-1.
, y =-1. 
, y =-1.
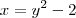

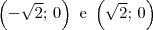
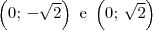

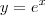
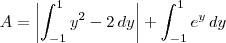


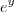 tem o maior valor da função em
tem o maior valor da função em  do que a função
do que a função 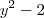 ,então o limite de integração superior é
,então o limite de integração superior é 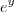 e o limite inferior é
e o limite inferior é 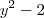 , e os limites de y serão
, e os limites de y serão  e
e  , conforme o gráfico.
, conforme o gráfico.