 por Danilo » Sáb Nov 09, 2013 18:42
por Danilo » Sáb Nov 09, 2013 18:42
Encontrar a área da região delimitada pelos gráficos
![y = \sqrt[]{x+2}, y = \frac{1}{x+1} , x = 2. y = \sqrt[]{x+2}, y = \frac{1}{x+1} , x = 2.](/latexrender/pictures/2eb41244b612117d9defccd9ef31b898.png)
Jogando o gráfico no geogebra e observando, uma das minhas dúvidas é se a seguinte integral está correta (a integral que me deve dar a área)
![\int_{0}^{2} \sqrt[]{x+2}- \frac{1}{x+1}dx \int_{0}^{2} \sqrt[]{x+2}- \frac{1}{x+1}dx](/latexrender/pictures/e2aaa93f8764259320d7c7e2ad6b4fe5.png)
. Está correto?? Grato desde já
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Sex Nov 15, 2013 11:44
por e8group » Sex Nov 15, 2013 11:44
Danilo , na minha opinião , apenas alterando um dos limites de integração e mantendo o integrando (aqui vou denotar o mesmo por g(x) só p/ não ter que digitar toda expressão), obteríamos a expressão
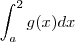
. Onde

é um número real (plotando as gráficos das funções , vemos que -1 < a < 0 ) que satisfaz a igualdade

.
Vamos aguarda a opinião dos demais membros do fórum .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral - Áreas
 por Danilo » Sex Nov 15, 2013 19:03
por Danilo » Sex Nov 15, 2013 19:03
- 2 Respostas
- 3526 Exibições
- Última mensagem por Man Utd

Qui Nov 21, 2013 17:20
Cálculo: Limites, Derivadas e Integrais
-
- Integral - Cálculo de áreas
por pinkfluor » Qui Jul 21, 2011 11:38
- 3 Respostas
- 2911 Exibições
- Última mensagem por pinkfluor

Qui Jul 21, 2011 17:21
Cálculo: Limites, Derivadas e Integrais
-
- Integral - Cálculo de áreas
 por AlbertoAM » Ter Jun 28, 2011 00:25
por AlbertoAM » Ter Jun 28, 2011 00:25
- 5 Respostas
- 6589 Exibições
- Última mensagem por AlbertoAM

Qua Jun 29, 2011 20:44
Cálculo: Limites, Derivadas e Integrais
-
- [Áreas] Integral Imprópria
por klueger » Qua Fev 27, 2013 09:40
- 1 Respostas
- 1866 Exibições
- Última mensagem por young_jedi

Qua Fev 27, 2013 13:55
Cálculo: Limites, Derivadas e Integrais
-
- [INTEGRAL] Cálculo de Áreas - Guidorizzi
por Lennon » Sáb Jun 08, 2013 02:24
- 2 Respostas
- 2830 Exibições
- Última mensagem por Lennon

Dom Jun 09, 2013 22:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![y = \sqrt[]{x+2}, y = \frac{1}{x+1} , x = 2. y = \sqrt[]{x+2}, y = \frac{1}{x+1} , x = 2.](/latexrender/pictures/2eb41244b612117d9defccd9ef31b898.png)
![\int_{0}^{2} \sqrt[]{x+2}- \frac{1}{x+1}dx \int_{0}^{2} \sqrt[]{x+2}- \frac{1}{x+1}dx](/latexrender/pictures/e2aaa93f8764259320d7c7e2ad6b4fe5.png) . Está correto?? Grato desde já
. Está correto?? Grato desde já
![y = \sqrt[]{x+2}, y = \frac{1}{x+1} , x = 2. y = \sqrt[]{x+2}, y = \frac{1}{x+1} , x = 2.](/latexrender/pictures/2eb41244b612117d9defccd9ef31b898.png)
![\int_{0}^{2} \sqrt[]{x+2}- \frac{1}{x+1}dx \int_{0}^{2} \sqrt[]{x+2}- \frac{1}{x+1}dx](/latexrender/pictures/e2aaa93f8764259320d7c7e2ad6b4fe5.png) . Está correto?? Grato desde já
. Está correto?? Grato desde já
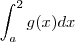 . Onde
. Onde  é um número real (plotando as gráficos das funções , vemos que -1 < a < 0 ) que satisfaz a igualdade
é um número real (plotando as gráficos das funções , vemos que -1 < a < 0 ) que satisfaz a igualdade  .
. 
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
