![\int_{}^{}\frac{sen(\sqrt[2]{\Theta})}{\sqrt[2]{\Theta{cos}^{3}(\sqrt[2]{\Theta})}}d\Theta \int_{}^{}\frac{sen(\sqrt[2]{\Theta})}{\sqrt[2]{\Theta{cos}^{3}(\sqrt[2]{\Theta})}}d\Theta](/latexrender/pictures/0ba7921d3d811e84af15cfe9d3b174af.png)
porém, a lista de exercício não apresenta resposta e eu cheguei neste resultado pelo método da substituição e por partes:
![\frac{4}{3}tg(\sqrt[2]{\Theta}){sec}^{\frac{3}{2}}(\sqrt[2]{\Theta})-\frac{8}{27}{sec}^{\frac{9}{2}}(\sqrt[2]{\Theta}) \frac{4}{3}tg(\sqrt[2]{\Theta}){sec}^{\frac{3}{2}}(\sqrt[2]{\Theta})-\frac{8}{27}{sec}^{\frac{9}{2}}(\sqrt[2]{\Theta})](/latexrender/pictures/c17c350e95eb03768bdc4584370b4ce5.png)
como não fiquei satisfeito em não saber se estava correto, tirei a prova real, derivando o resultado obtido acima cheguei em:
![\frac{3{tg}^{2}(\sqrt[2]{\Theta}){sec}^{\frac{3}{2}}(\sqrt[2]{\Theta})-2tg(\sqrt[2]{\Theta}){sec}^{\frac{9}{2}}(\sqrt[2]{\Theta})+2{sec}^{\frac{7}{2}}(\sqrt[2]{\Theta})}{3\sqrt[2]{\Theta}} \frac{3{tg}^{2}(\sqrt[2]{\Theta}){sec}^{\frac{3}{2}}(\sqrt[2]{\Theta})-2tg(\sqrt[2]{\Theta}){sec}^{\frac{9}{2}}(\sqrt[2]{\Theta})+2{sec}^{\frac{7}{2}}(\sqrt[2]{\Theta})}{3\sqrt[2]{\Theta}}](/latexrender/pictures/a0f59f149fdb92e96c700186e6db8822.png)
e pela "pequena" diferença entre a função original e a prova real conclui que estava errado (ah vá!) e agora peço ajuda para vocês, porque não tenho a mínima ideia de como resolver este exercício.
Obrigado


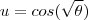
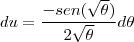
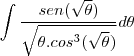
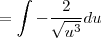
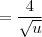
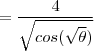


 .
.
 :
: