 por Sobreira » Qua Out 02, 2013 11:32
por Sobreira » Qua Out 02, 2013 11:32
Amigos,
Fiz uma prova de cálculo 3 e havia uma sequência e o exercício pedia para determinar o limite da seguinte sequência:
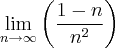
Então resolvi por maior grau:

Logo:
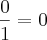
Mas o professor me descontou metade da questão pois informou que a resposta estava correta mas o método de resolução errado



Que erro há nesta resolução ???
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por Leticia_alves » Qua Out 02, 2013 16:01
por Leticia_alves » Qua Out 02, 2013 16:01
Bom, temos o seguinte limite:
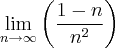
.
Por ser uma indeterminação, utilizamos a Regra de L'Hospital, assim:
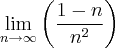
=
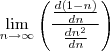
=

= =

O limite do quociente é o quociente dos limites:
Como o limite de constante é constante:

E, como o limite de n quando n tende ao infinito é infinito, segue que:
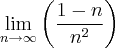
= 0.
Não sei se é isso que o seu professor queria, mas só consigo enxergar esse método de resolução.
Espero ter ajudado!
Abraços
-
Leticia_alves
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Sex Jun 14, 2013 19:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Sobreira » Qua Out 02, 2013 17:30
por Sobreira » Qua Out 02, 2013 17:30
Então. Entendo que L´Hospital seria uma técnica a mais para resolver limites que não são facilmente resolvidos por fatoração, por exemplo. Posso utilizar perfeitamente L´Hospital, mas entendo que este limite seria também tranquilamente resolvido por alguma técnica mais simples (como dividir uma equação racional pelo maior grau de x, neste caso).
Então, utilizando esta técnica (imagino que efetuei o cálculo de forma correta) chego ao desenvolvimento do limite. Isto que gostaria de saber, se meu cálculo através desta técnica estaria correta ou não.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Cálculo de Limite] Resolução de um limite
por julianocoutinho » Seg Mai 13, 2013 01:47
- 3 Respostas
- 3322 Exibições
- Última mensagem por Man Utd

Qua Mai 15, 2013 22:26
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] RESOLUÇÃO
por beel » Sex Set 02, 2011 15:14
- 2 Respostas
- 1707 Exibições
- Última mensagem por beel

Dom Out 16, 2011 17:03
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] RESOLUÇÃO 2
por beel » Sex Set 02, 2011 17:58
- 2 Respostas
- 1704 Exibições
- Última mensagem por beel

Dom Out 16, 2011 17:03
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] RESOLUÇÃO 3
por beel » Sáb Set 03, 2011 20:17
- 8 Respostas
- 4751 Exibições
- Última mensagem por beel

Dom Set 04, 2011 15:32
Cálculo: Limites, Derivadas e Integrais
-
- Resolução de Limite
por Ewerton Farias » Ter Abr 24, 2012 02:11
- 2 Respostas
- 2074 Exibições
- Última mensagem por Ewerton Farias

Sex Abr 27, 2012 17:30
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
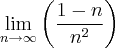

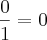


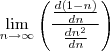






 , avisa que eu resolvo.
, avisa que eu resolvo.

