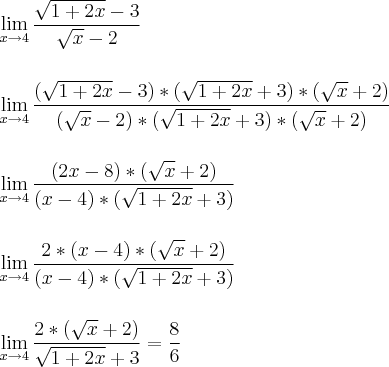por vamola » Sáb Set 28, 2013 19:04
por vamola » Sáb Set 28, 2013 19:04
Fala pessoal, tudo bem? Tô tendo dificuldade em resolver esse limite:
![\lim_{x \rightarrow 4} \frac{ \sqrt[2]{1+2x}-3}{\sqrt[2]{x}-2} \lim_{x \rightarrow 4} \frac{ \sqrt[2]{1+2x}-3}{\sqrt[2]{x}-2}](/latexrender/pictures/375f256de85502e56a2b3d3dc6405bc0.png)
A resposta é
4/3.
Eu sei resolver por conjugado, quando tem raíz só em cima ou só embaixo é tranquilo, mas com raíz em cima e embaixo não to conseguindo não...como proceder?
Obrigado.
Editado pela última vez por
vamola em Sáb Set 28, 2013 20:40, em um total de 1 vez.
-
vamola
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Set 28, 2013 18:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Man Utd » Sáb Set 28, 2013 19:55
por Man Utd » Sáb Set 28, 2013 19:55
vamola escreveu:Fala pessoal, tudo bem? Tô tendo dificuldade em resolver esse limite:
![\lim_{x \rightarrow 4} \frac{ \sqrt[2]{1+2x}}{\sqrt[2]{x}-2} \lim_{x \rightarrow 4} \frac{ \sqrt[2]{1+2x}}{\sqrt[2]{x}-2}](/latexrender/pictures/64b4357c2bdb3b694ab8be95ddb94028.png)
A resposta é
4/3.
Eu sei resolver por conjugado, quando tem raíz só em cima ou só embaixo é tranquilo, mas com raíz em cima e embaixo não to conseguindo não...como proceder?
Obrigado.
amigo,favor verificar o enunciado se o limite for este,então não existe limite, conforme o wolfram :
http://www.wolframalpha.com/input/?i=li ... 9%2Cx-%3E4
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por vamola » Sáb Set 28, 2013 20:41
por vamola » Sáb Set 28, 2013 20:41
Realmente, tava faltando um -3. Agora corrigi.
E se possível me explicar sem utilizar L'Hopital seria melhor...eu até sei aplicar, mas como se trata de uma prova de limites, o professor não permite o uso do mesmo.
Valeu!
-
vamola
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Set 28, 2013 18:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por vamola » Dom Set 29, 2013 19:10
por vamola » Dom Set 29, 2013 19:10
Perfeito. Obrigado.
-
vamola
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Set 28, 2013 18:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] Como resolver raiz dentro de raiz ?
 por natyncb » Qui Abr 12, 2012 00:31
por natyncb » Qui Abr 12, 2012 00:31
- 10 Respostas
- 13772 Exibições
- Última mensagem por LuizAquino

Sex Ago 24, 2012 07:50
Cálculo: Limites, Derivadas e Integrais
-
- [limites] reciso de ajuda nessa questão de limites raiz quad
por alexia » Ter Nov 15, 2011 19:55
- 1 Respostas
- 5406 Exibições
- Última mensagem por LuizAquino

Qua Nov 16, 2011 15:16
Cálculo: Limites, Derivadas e Integrais
-
- Limites com raiz no numerador
por liliars » Qua Jul 07, 2010 16:34
- 4 Respostas
- 13107 Exibições
- Última mensagem por elinesena

Sáb Nov 24, 2012 15:22
Cálculo: Limites, Derivadas e Integrais
-
- [Limites de funções com raíz]
por yakini » Dom Fev 10, 2013 11:32
- 2 Respostas
- 1891 Exibições
- Última mensagem por yakini

Dom Fev 10, 2013 16:17
Cálculo: Limites, Derivadas e Integrais
-
- [Limites envolvendo Raiz]
por jeferson lopes » Ter Mar 26, 2013 12:14
- 1 Respostas
- 1563 Exibições
- Última mensagem por e8group

Ter Mar 26, 2013 13:02
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x \rightarrow 4} \frac{ \sqrt[2]{1+2x}-3}{\sqrt[2]{x}-2} \lim_{x \rightarrow 4} \frac{ \sqrt[2]{1+2x}-3}{\sqrt[2]{x}-2}](/latexrender/pictures/375f256de85502e56a2b3d3dc6405bc0.png)

![\lim_{x \rightarrow 4} \frac{ \sqrt[2]{1+2x}-3}{\sqrt[2]{x}-2} \lim_{x \rightarrow 4} \frac{ \sqrt[2]{1+2x}-3}{\sqrt[2]{x}-2}](/latexrender/pictures/375f256de85502e56a2b3d3dc6405bc0.png)