na letra c temos que:
![\gamma\left( t\right)= (cos t,sen t, {e}^{-t}) , t \in[0,\pi] \gamma\left( t\right)= (cos t,sen t, {e}^{-t}) , t \in[0,\pi]](/latexrender/pictures/99acdebcd051384e61cccd716c6d65d3.png)
desenvolvi e travei nessa integral abaixo:
![\int_{0}^{\pi}\sqrt[]{{e}^{-2t}+1}dt \int_{0}^{\pi}\sqrt[]{{e}^{-2t}+1}dt](/latexrender/pictures/38fb2bab62d0b438aafb68c1d58ed022.png)
gostaria que alguém me ajudasse a resolver.
1) tenho que transformar em uma substituição trigonométrica, portanto
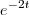 substituirei por
substituirei por  , logo, teremos
, logo, teremos ![\sqrt[]{{tg^{2} \left(u \right)}+ 1} \sqrt[]{{tg^{2} \left(u \right)}+ 1}](/latexrender/pictures/088411e6a74e19a508562777e40598f7.png) que resultará em
que resultará em 
Para isso
 e
e 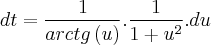
Os limites serão
 será
será  que será
que será  e
e  será
será 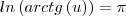 , logo
, logo 
Gostaria de saber se há algum passo errado e como faço pra achar essa integral:
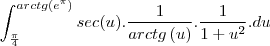


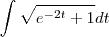



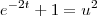
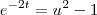
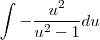
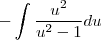
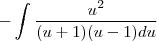
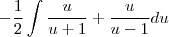

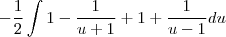
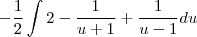
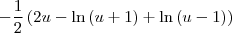


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)