 por Sobreira » Qui Set 26, 2013 09:06
por Sobreira » Qui Set 26, 2013 09:06
Tenho dificuldade em reconhecer quando uma E.D.O é separável ou não. Sei que ela deve se apresentar desta forma:
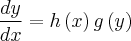
Mas não tenho total certeza sobre como tentar separar uma E.D.O corretamente.
Por exemplo, as equações a seguir eu resolvi por fator integrante mas acho que consigo separar. Consigo ou não ??


Onde

são constantes.
Já nesta equação qual a diferença, em relação a separação, das formas abaixo:


"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por young_jedi » Qui Set 26, 2013 14:19
por young_jedi » Qui Set 26, 2013 14:19
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Sobreira » Sáb Set 28, 2013 09:25
por Sobreira » Sáb Set 28, 2013 09:25
young_jedi escreveu:esta primeira não da para separar


veja que não da para separar em uma função de y vezes uma função de x
Então...aí que está.
Eu não consigo entender como é possível verificar se as funções irão se apresentar como produto ou não.
Pelo que eu entendi não pode haver soma entre

e

???
Neste termo eles estão digamos amarrados??? mas e se eu expandir não vou ter a separação???
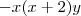
Por exemplo:

E daí eu poderia separar ???
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por young_jedi » Sáb Set 28, 2013 11:44
por young_jedi » Sáb Set 28, 2013 11:44
este termo você consegue seperar
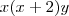
o problema é que também temos uma exponencial de x

por isso você não consegue separar
realmente você não pode ter uma soma entre x e y por exemplo

essa função você também não consegue separar
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Sobreira » Sáb Set 28, 2013 12:46
por Sobreira » Sáb Set 28, 2013 12:46
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por young_jedi » Sáb Set 28, 2013 18:13
por young_jedi » Sáb Set 28, 2013 18:13
esta certo a partir dai não da para separar mais!!!
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Solução de uma Equação diferencial ordinaria
por thejotta » Seg Jan 14, 2013 00:03
- 0 Respostas
- 1020 Exibições
- Última mensagem por thejotta

Seg Jan 14, 2013 00:03
Cálculo: Limites, Derivadas e Integrais
-
- Equação Diferencial.
por Higor » Seg Fev 21, 2011 13:12
- 4 Respostas
- 12206 Exibições
- Última mensagem por Higor

Seg Fev 21, 2011 14:46
Cálculo: Limites, Derivadas e Integrais
-
- Equaçao diferencial
por romulo39 » Dom Abr 03, 2011 20:58
- 1 Respostas
- 3940 Exibições
- Última mensagem por LuizAquino

Seg Abr 04, 2011 14:39
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial
por jacquelline » Qui Mai 17, 2012 11:04
- 2 Respostas
- 2072 Exibições
- Última mensagem por jacquelline

Sáb Mai 19, 2012 20:37
Cálculo: Limites, Derivadas e Integrais
-
- Equação diferencial - 1
por Cleyson007 » Qua Nov 07, 2012 21:09
- 8 Respostas
- 3844 Exibições
- Última mensagem por MarceloFantini

Qui Nov 08, 2012 17:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
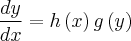


 são constantes.
são constantes.





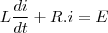

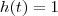 e
e 
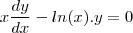

 e
e 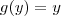
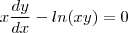

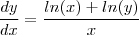
 e
e  ???
???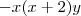

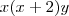






 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.