 por duduscs » Dom Set 22, 2013 21:10
por duduscs » Dom Set 22, 2013 21:10
Olá pessoal, sou novo no fórum e vim porque necessito de ajuda em uma questão, pois não estou conseguindo resolver.
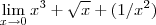
e também este:
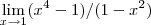
Obrigado.
-
duduscs
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Set 22, 2013 21:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. De Computação
- Andamento: cursando
 por Sobreira » Seg Set 23, 2013 12:25
por Sobreira » Seg Set 23, 2013 12:25
Note que no primeiro exemplo você terá uma indeterminação do tipo

, portanto você irá obter como resposta uma função tendendo a

.
Você pode verificar se a função tende a +

ou -

, através dos limites laterais, mas como

, logo por qualquer lado será positivo e a resposta será +

.
No segundo exemplo há uma indeterminação do tipo

, portanto você deve utilizar alguma técnica (fatoração por exemplo) para eliminar a indeterminação:
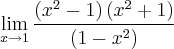
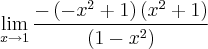
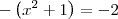
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por duduscs » Seg Set 23, 2013 13:08
por duduscs » Seg Set 23, 2013 13:08
Sobreira escreveu:Note que no primeiro exemplo você terá uma indeterminação do tipo

, portanto você irá obter como resposta uma função tendendo a

.
Você pode verificar se a função tende a +

ou -

, através dos limites laterais, mas como

, logo por qualquer lado será positivo e a resposta será +

.
No segundo exemplo há uma indeterminação do tipo

, portanto você deve utilizar alguma técnica (fatoração por exemplo) para eliminar a indeterminação:
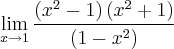
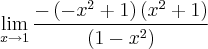
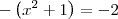
O segundo exemplo eu entendi.
Mas em relação ao primeiro, não haverá limite, correto? Pois se analisar o limite pela direita, ele tenderá ao +infinito, porém, se analisar pela esquerda, ou seja, valores menores que zero, e consequentemente negativos, não haverá limite lateral devido à

?
-
duduscs
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Set 22, 2013 21:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Eng. De Computação
- Andamento: cursando
 por Sobreira » Ter Set 24, 2013 01:47
por Sobreira » Ter Set 24, 2013 01:47
Então...acabei analisando rápido e nem prestei atenção à raíz, então neste caso, mesmo pela esquerda e sendo negativo eu elevaria ao quadrado e obteria infinito positivo. Mas sua observação é pertinente, o limite não existe pela esquerda devido à raíz.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite trigonométrico] Como calculo este limite?
por Ronaldobb » Qua Nov 07, 2012 23:14
- 3 Respostas
- 5118 Exibições
- Última mensagem por Ronaldobb

Qui Nov 08, 2012 07:37
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] - Dúvida sobre o resultado de um limite
por Paulo Souza » Dom Ago 25, 2013 20:57
- 0 Respostas
- 1839 Exibições
- Última mensagem por Paulo Souza

Dom Ago 25, 2013 20:57
Cálculo: Limites, Derivadas e Integrais
-
- [LIMITE] Dúvida sobre provar pela definição
por Icaro1931 » Qui Mai 23, 2013 22:14
- 1 Respostas
- 1483 Exibições
- Última mensagem por e8group

Sex Mai 24, 2013 08:59
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Como calcular este limite?
por alienpuke » Qui Out 01, 2015 11:18
- 1 Respostas
- 1930 Exibições
- Última mensagem por nakagumahissao

Qui Out 01, 2015 23:59
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Como calcular este limite?
por alienpuke » Qua Set 30, 2015 23:32
- 1 Respostas
- 1974 Exibições
- Última mensagem por nakagumahissao

Sex Out 02, 2015 00:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
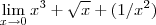
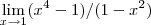

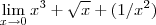
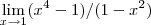

 , portanto você irá obter como resposta uma função tendendo a
, portanto você irá obter como resposta uma função tendendo a  .
. ou -
ou - , através dos limites laterais, mas como
, através dos limites laterais, mas como  , logo por qualquer lado será positivo e a resposta será +
, logo por qualquer lado será positivo e a resposta será + .
. , portanto você deve utilizar alguma técnica (fatoração por exemplo) para eliminar a indeterminação:
, portanto você deve utilizar alguma técnica (fatoração por exemplo) para eliminar a indeterminação: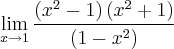
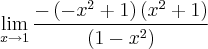
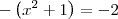

, portanto você irá obter como resposta uma função tendendo a
.
ou -
, através dos limites laterais, mas como
, logo por qualquer lado será positivo e a resposta será +
.
, portanto você deve utilizar alguma técnica (fatoração por exemplo) para eliminar a indeterminação:
 ?
?

