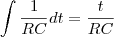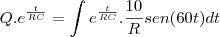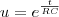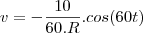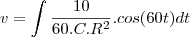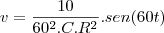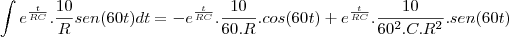por FernandaOliveira » Dom Ago 25, 2013 20:52
por FernandaOliveira » Dom Ago 25, 2013 20:52
Questão 3: Considere um circuito elétrico modelado pela equação diferencial R dQ/dt + 1Q/C = E(t)
que contem um capacitor com capacitância de C Farads (F); um resistor
com uma resistência de R ohms (

); com carga Q medida em coulombs; voltagem E(t)
medida em volts e o tempo t medido em segundos.
Supondo que , R=2

, C=0,01 F, Q(0)=0 e E(t)=10sen (60t), calcule a carga e a corrente i
no instante t. (observação a corrente i é dada por i = dQ/dt ).
Me ajudem por favor é urgente preciso enviar a prova até dia 27/08 terça feira.
-
FernandaOliveira
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Dom Ago 25, 2013 20:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por young_jedi » Seg Ago 26, 2013 16:22
por young_jedi » Seg Ago 26, 2013 16:22
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equações diferenciais
por tiagofabre » Sex Set 21, 2012 00:48
- 1 Respostas
- 1860 Exibições
- Última mensagem por MarceloFantini

Sex Set 21, 2012 01:14
Cálculo: Limites, Derivadas e Integrais
-
- equacoes diferenciais
por Thais Bomfim » Qua Dez 12, 2012 01:58
- 2 Respostas
- 2192 Exibições
- Última mensagem por Thais Bomfim

Qua Dez 12, 2012 14:02
Equações
-
- Equações Diferenciais
por sergio2205 » Qua Mar 06, 2013 13:27
- 1 Respostas
- 1733 Exibições
- Última mensagem por Russman

Qua Mar 06, 2013 15:14
Equações
-
- Equações Diferenciais
por marinalcd » Sex Ago 09, 2013 15:19
- 1 Respostas
- 1632 Exibições
- Última mensagem por Man Utd

Dom Jun 15, 2014 17:40
Cálculo: Limites, Derivadas e Integrais
-
- Equações Diferenciais
por FernandaOliveira » Dom Ago 25, 2013 20:42
- 1 Respostas
- 1665 Exibições
- Última mensagem por FernandaOliveira

Qua Ago 28, 2013 16:41
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ); com carga Q medida em coulombs; voltagem E(t)
); com carga Q medida em coulombs; voltagem E(t)  , C=0,01 F, Q(0)=0 e E(t)=10sen (60t), calcule a carga e a corrente i
, C=0,01 F, Q(0)=0 e E(t)=10sen (60t), calcule a carga e a corrente i