[Integral de Linha] Segmento de reta

[Claudin]

Olá, to com uma duvida em como resolver integral de linha

Calcule a seguinte integral



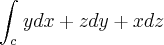
onde C consiste n segmento de reta que une (2,0,0) a (3,4,5) seguido pelo segmento de reta vertical 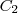de (3,4,5) a (3,4,0).

Não estou conseguindo parametrizar utilizando aquela fórmula de segmento de reta, acho que esse é o problema.

Obrigado

[MateusL]

Vamos supor que queres um segmento de reta que une dois pontos pontos e .

A reta que contém esse segmento pode ser representada como:



O segmento procurado é o conjunto de pontos pertencentes a , com o parâmetro variando no intervalo .
Ou seja:



Só tens que notar que nessa integral que queres calcular, terás que dividí-la em duas: uma integral para e outra para .
Abraço!