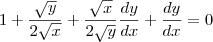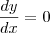por mthc10 » Qui Jun 06, 2013 22:03
por mthc10 » Qui Jun 06, 2013 22:03
Bem, deparei-me com a seguinte questão:
Em que ponto da curva
![x + \sqrt[2]{xy} + y = 1 x + \sqrt[2]{xy} + y = 1](/latexrender/pictures/00aa3e853f9fd18a58b9ee1d9b0af8d0.png)
a reta tangente é paralela ao eixo x ?
Derivei implicitamente e ficou assim:
![1 + \frac{\sqrt[]{y}}{2\sqrt[]{x}} + \frac{\sqrt[]{x}}{2\sqrt[]{y}}.\frac{dy}{dx} + \frac{dy}{dx} = 0 1 + \frac{\sqrt[]{y}}{2\sqrt[]{x}} + \frac{\sqrt[]{x}}{2\sqrt[]{y}}.\frac{dy}{dx} + \frac{dy}{dx} = 0](/latexrender/pictures/cb51d2af5da69faf3752623d4d4fc6a2.png)
Daí em diante não sei o que fazer...
Alguém pode me ajudar ?
-
mthc10
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mai 21, 2013 23:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharel em Engenharia Elétrica
- Andamento: cursando
 por young_jedi » Sáb Jun 08, 2013 12:38
por young_jedi » Sáb Jun 08, 2013 12:38
Amigo eu calculei a derivada implícita obtemos

que pode ser expresso por
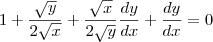
ate ai tudo certo
nos temos que como a reta tangente é paralela ao eixo x então a derivada da função nesse ponto é 0 portanto
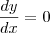
substitua esse valor na equação e encontre os pontos em que a equação é satisfeita
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Reta Paralela à Reta Tangente]
por raimundoocjr » Qui Mai 30, 2013 18:44
- 0 Respostas
- 1150 Exibições
- Última mensagem por raimundoocjr

Qui Mai 30, 2013 18:44
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] Reta tangente e Reta perpendicular
por antonelli2006 » Ter Nov 22, 2011 11:21
- 1 Respostas
- 8666 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 14:28
Cálculo: Limites, Derivadas e Integrais
-
- Calcular lado de uma figura formada por uma recta paralela
por LBT » Dom Dez 05, 2010 17:22
- 2 Respostas
- 2002 Exibições
- Última mensagem por LBT

Seg Dez 06, 2010 05:35
Geometria Analítica
-
- Derivada - Reta tangente
por emsbp » Qua Mai 02, 2012 18:28
- 2 Respostas
- 1914 Exibições
- Última mensagem por emsbp

Qui Mai 03, 2012 11:38
Cálculo: Limites, Derivadas e Integrais
-
- Derivada, equação da reta
por Ana Cristina Lopes » Sáb Jun 15, 2013 19:54
- 1 Respostas
- 2434 Exibições
- Última mensagem por young_jedi

Sáb Jun 15, 2013 23:27
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![x + \sqrt[2]{xy} + y = 1 x + \sqrt[2]{xy} + y = 1](/latexrender/pictures/00aa3e853f9fd18a58b9ee1d9b0af8d0.png) a reta tangente é paralela ao eixo x ?
a reta tangente é paralela ao eixo x ?![1 + \frac{\sqrt[]{y}}{2\sqrt[]{x}} + \frac{\sqrt[]{x}}{2\sqrt[]{y}}.\frac{dy}{dx} + \frac{dy}{dx} = 0 1 + \frac{\sqrt[]{y}}{2\sqrt[]{x}} + \frac{\sqrt[]{x}}{2\sqrt[]{y}}.\frac{dy}{dx} + \frac{dy}{dx} = 0](/latexrender/pictures/cb51d2af5da69faf3752623d4d4fc6a2.png)

![x + \sqrt[2]{xy} + y = 1 x + \sqrt[2]{xy} + y = 1](/latexrender/pictures/00aa3e853f9fd18a58b9ee1d9b0af8d0.png) a reta tangente é paralela ao eixo x ?
a reta tangente é paralela ao eixo x ?![1 + \frac{\sqrt[]{y}}{2\sqrt[]{x}} + \frac{\sqrt[]{x}}{2\sqrt[]{y}}.\frac{dy}{dx} + \frac{dy}{dx} = 0 1 + \frac{\sqrt[]{y}}{2\sqrt[]{x}} + \frac{\sqrt[]{x}}{2\sqrt[]{y}}.\frac{dy}{dx} + \frac{dy}{dx} = 0](/latexrender/pictures/cb51d2af5da69faf3752623d4d4fc6a2.png)