 por Jasbinschek » Qua Mai 29, 2013 01:17
por Jasbinschek » Qua Mai 29, 2013 01:17
Então, eu peguei uma integral hoje que eu não consegui resolver, procurei na internet e achei o resultado dela, mas eu gostaria de saber o motivo, como eu chego nela?
o nosso querido Wolfram me disse isso:
http://www.wolframalpha.com/input/?i=in ... -x%29%29dxa integral é a seguinte:

alguém pode me explicar como isso funciona?
obrigado.
-
Jasbinschek
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Mai 29, 2013 01:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da comp.
- Andamento: cursando
 por temujin » Qua Mai 29, 2013 11:04
por temujin » Qua Mai 29, 2013 11:04
Acho que dá pra fazer por partes.
Vejamos:


Agora, um detalhe. Essa é uma função gamma, né? Se integrar de 0 a mais infinito ela vai ter essa cara:

Eu não conheço a demonstração, mas acho que não deve ser difícil de encontrar.
-
temujin
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Qui Mar 14, 2013 15:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: formado
 por Jasbinschek » Qua Mai 29, 2013 20:11
por Jasbinschek » Qua Mai 29, 2013 20:11
Eu tentei por partes, mas na parte que fica integral de Vdu é
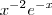
afinal o u tem que ser igual a
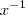
então cresce infinitamente...
e sim, é uma função gamma
-
Jasbinschek
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Mai 29, 2013 01:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da comp.
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral com exponencial
por suziquim » Ter Mai 10, 2011 18:07
- 2 Respostas
- 3219 Exibições
- Última mensagem por suziquim

Qua Mai 11, 2011 11:08
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Exponencial
por raulalves_ » Qua Abr 18, 2012 01:49
- 1 Respostas
- 1657 Exibições
- Última mensagem por LuizAquino

Qui Abr 19, 2012 14:59
Cálculo: Limites, Derivadas e Integrais
-
- (integral) função exponencial
por manuel_pato1 » Sex Dez 07, 2012 20:08
- 6 Respostas
- 3845 Exibições
- Última mensagem por manuel_pato1

Sáb Dez 08, 2012 15:02
Cálculo: Limites, Derivadas e Integrais
-
- integral de função exponencial
por vivima » Sex Mai 09, 2014 13:36
- 2 Respostas
- 2007 Exibições
- Última mensagem por vivima

Sex Mai 09, 2014 15:19
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] integral definida com exponencial
por beel » Dom Nov 20, 2011 22:38
- 3 Respostas
- 2917 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 16:55
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.








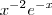 afinal o u tem que ser igual a
afinal o u tem que ser igual a 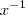


 .
.
 :
: