 por Ge_dutra » Qui Mai 09, 2013 01:06
por Ge_dutra » Qui Mai 09, 2013 01:06
Boa noite, estou começando agora meus estudos sobre integral e tenho algumas dúvidas básicas.
Por exemplo na seguinte questão:
![\int_{-1}^{1}\left(({\sqrt[3]{t}})^{2} -2\right)dt \int_{-1}^{1}\left(({\sqrt[3]{t}})^{2} -2\right)dt](/latexrender/pictures/3ba779ea87368f0c99e1912d78bdfe19.png)
, é para resolver por substituição; tentei colocar o
![\sqrt[3]{t} \sqrt[3]{t}](/latexrender/pictures/d3a30e3fd87bd1c2aa7b090fade6b05c.png)
como sendo o meu
u, mas não deu mt certo.
Então, como resolver?
Desde já agradeço.
-
Ge_dutra
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Jan 28, 2013 09:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Russman » Qui Mai 09, 2013 01:48
por Russman » Qui Mai 09, 2013 01:48
Lembre-se que
![\left (\sqrt[3]{t} \right )^{2} = t^{\frac{2}{3}} \left (\sqrt[3]{t} \right )^{2} = t^{\frac{2}{3}}](/latexrender/pictures/e2e0b607af624eaf21df0ad16716a963.png)
,
que
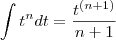
e que

.
Com isso voce consegue resolver a questão.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Ge_dutra » Sáb Mai 11, 2013 18:10
por Ge_dutra » Sáb Mai 11, 2013 18:10
Perdão, mas ainda não deu certo. Talvez eu esteja errando em conta, já que encontrei o dobro do valor, mas não estou enxergando o erro. Poderia especificar as contas por favor?
-
Ge_dutra
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Jan 28, 2013 09:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Resolver Integral definida com trigonometria
por rodrigoboreli » Dom Set 07, 2014 01:02
- 1 Respostas
- 4341 Exibições
- Última mensagem por adauto martins

Sex Out 17, 2014 12:39
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo Integral] Integral Definida
por ARCS » Sáb Fev 02, 2013 21:37
- 2 Respostas
- 3671 Exibições
- Última mensagem por e8group

Sáb Fev 02, 2013 22:13
Cálculo: Limites, Derivadas e Integrais
-
- [integral] integral definida por partes
por gabriel feron » Seg Mar 11, 2013 00:48
- 2 Respostas
- 3063 Exibições
- Última mensagem por gabriel feron

Seg Mar 11, 2013 18:19
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Derivar integral definida
por troziinho » Ter Mar 31, 2015 20:26
- 0 Respostas
- 2498 Exibições
- Última mensagem por troziinho

Ter Mar 31, 2015 20:26
Cálculo: Limites, Derivadas e Integrais
-
- Integral definida
por exploit » Ter Set 07, 2010 19:17
- 4 Respostas
- 3617 Exibições
- Última mensagem por exploit

Qua Set 08, 2010 19:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{-1}^{1}\left(({\sqrt[3]{t}})^{2} -2\right)dt \int_{-1}^{1}\left(({\sqrt[3]{t}})^{2} -2\right)dt](/latexrender/pictures/3ba779ea87368f0c99e1912d78bdfe19.png) , é para resolver por substituição; tentei colocar o
, é para resolver por substituição; tentei colocar o ![\sqrt[3]{t} \sqrt[3]{t}](/latexrender/pictures/d3a30e3fd87bd1c2aa7b090fade6b05c.png) como sendo o meu u, mas não deu mt certo.
como sendo o meu u, mas não deu mt certo.
![\int_{-1}^{1}\left(({\sqrt[3]{t}})^{2} -2\right)dt \int_{-1}^{1}\left(({\sqrt[3]{t}})^{2} -2\right)dt](/latexrender/pictures/3ba779ea87368f0c99e1912d78bdfe19.png) , é para resolver por substituição; tentei colocar o
, é para resolver por substituição; tentei colocar o ![\sqrt[3]{t} \sqrt[3]{t}](/latexrender/pictures/d3a30e3fd87bd1c2aa7b090fade6b05c.png) como sendo o meu u, mas não deu mt certo.
como sendo o meu u, mas não deu mt certo.
![\left (\sqrt[3]{t} \right )^{2} = t^{\frac{2}{3}} \left (\sqrt[3]{t} \right )^{2} = t^{\frac{2}{3}}](/latexrender/pictures/e2e0b607af624eaf21df0ad16716a963.png) ,
, 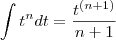 e que
e que .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.