Uma caixa d’agua no formato de um cilindro circular reto de raio r e altura h será construída em cima de um prédio onde o teto tem formato de um cone de revolução com raio R e altura H, conforme a figura abaixo.
A figura é um cilindro circular reto inscrito num cone reto. Onde o r e o h são o raio e a altura do cilindro e o R e H o raio e altura do cone.
Colocando valores como exemplo para a formula : R vale 5 m, e H vale 12 m.
encontrar as dimensões de r (em função de R e H) que maximiza a área total da superfície da caixa d’ água (inclusive a base inferior).
Questões:
Tem como solucionar a situação sem a aplicação das derivadas?
Qual as dimensões de r (em função de R e H) que maximiza a área total da superfície da caixa d’ água (inclusive a base inferior)?
Qual a solução gráfica para a questao?


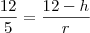
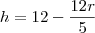
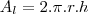
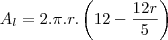
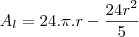




 . Você esqueceu de levar o
. Você esqueceu de levar o 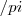 com a fração.
com a fração.



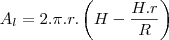
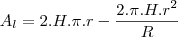
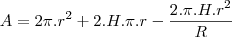
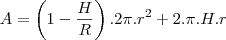



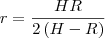
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)