 por Russman » Sáb Abr 27, 2013 18:23
por Russman » Sáb Abr 27, 2013 18:23
o que voce tentou fazer? O 1° passo é calcular a derivada da função. Voce o fez?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por xafabi » Sáb Abr 27, 2013 20:46
por xafabi » Sáb Abr 27, 2013 20:46
Ola amigo daqui para frente nao sei mais
y' = (cosx - x. senx) e^{x.cosx}
-
xafabi
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Abr 02, 2013 22:40
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Russman » Dom Abr 28, 2013 23:28
por Russman » Dom Abr 28, 2013 23:28
Agora, suponha que a equação da reta tangente seja
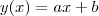
, onde o valor

é a derivada aplicada no ponto - faça x=1 na derivada- e o valor

voce calcula impondo que a coordenada

no ponto é igual para a reta e para a função.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por xafabi » Seg Abr 29, 2013 08:45
por xafabi » Seg Abr 29, 2013 08:45
Amigo poderia ajudar não to conseguindo
-
xafabi
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Abr 02, 2013 22:40
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por xafabi » Seg Abr 29, 2013 20:46
por xafabi » Seg Abr 29, 2013 20:46
Ola pessoa ajuda ae , tenho que entregar amanha e nao sei como fazer, senão vou tirar um 0, estou estudando essa materia so esse semestre e nunca mais vou estudar, se puderem ajudar, agradeço muito
-
xafabi
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Abr 02, 2013 22:40
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [DERIVADA] Reta tangente e Reta perpendicular
por antonelli2006 » Ter Nov 22, 2011 11:21
- 1 Respostas
- 8669 Exibições
- Última mensagem por LuizAquino

Ter Nov 22, 2011 14:28
Cálculo: Limites, Derivadas e Integrais
-
- [Reta Paralela à Reta Tangente]
por raimundoocjr » Qui Mai 30, 2013 18:44
- 0 Respostas
- 1153 Exibições
- Última mensagem por raimundoocjr

Qui Mai 30, 2013 18:44
Cálculo: Limites, Derivadas e Integrais
-
- Reta tangente
por AlbertoAM » Sáb Abr 30, 2011 15:32
- 1 Respostas
- 1528 Exibições
- Última mensagem por FilipeCaceres

Sáb Abr 30, 2011 19:13
Cálculo: Limites, Derivadas e Integrais
-
- Reta tangente
por AlbertoAM » Dom Mai 01, 2011 19:22
- 3 Respostas
- 2019 Exibições
- Última mensagem por LuizAquino

Seg Mai 02, 2011 20:02
Cálculo: Limites, Derivadas e Integrais
-
- Reta tangente
por alzenir agapito » Ter Mai 17, 2011 22:55
- 2 Respostas
- 1677 Exibições
- Última mensagem por Maykids

Qui Mai 19, 2011 12:36
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





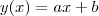 , onde o valor
, onde o valor  é a derivada aplicada no ponto - faça x=1 na derivada- e o valor
é a derivada aplicada no ponto - faça x=1 na derivada- e o valor  voce calcula impondo que a coordenada
voce calcula impondo que a coordenada  no ponto é igual para a reta e para a função.
no ponto é igual para a reta e para a função.



 .
.
 :
: