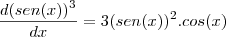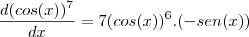por Danilo » Ter Abr 23, 2013 11:51
por Danilo » Ter Abr 23, 2013 11:51
Calcular a derivada de

tentei fazer assim:
derivada de

=
![\left[{\left(senx \right)}^{3} \right] - \left[{\left(cosx \right)}^{7} \right] \left[{\left(senx \right)}^{3} \right] - \left[{\left(cosx \right)}^{7} \right]](/latexrender/pictures/4da6df81b35355fd2435511458c74605.png)
=

mas essa não é a resposta correta eu não sei onde está eu erro. E eu também não consegui colocar o símbolo de derivada.
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Dúvida ao calcular uma derivada...
por dileivas » Ter Mai 01, 2012 09:54
- 2 Respostas
- 2258 Exibições
- Última mensagem por dileivas

Ter Mai 01, 2012 17:18
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] Duvida em derivada da definição.
por paulohenrique_ » Dom Dez 09, 2012 16:05
- 1 Respostas
- 1931 Exibições
- Última mensagem por young_jedi

Dom Dez 09, 2012 18:12
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida em derivada
por luiz3107 » Seg Ago 23, 2010 02:50
- 2 Respostas
- 1918 Exibições
- Última mensagem por luiz3107

Seg Ago 23, 2010 15:15
Cálculo: Limites, Derivadas e Integrais
-
- Derivada duvida
por Isabela Sa » Ter Jul 12, 2011 11:46
- 5 Respostas
- 2726 Exibições
- Última mensagem por LuizAquino

Qua Jul 13, 2011 10:07
Cálculo: Limites, Derivadas e Integrais
-
- Duvida Derivada.
por Bio10ct » Qua Abr 18, 2012 09:17
- 1 Respostas
- 1052 Exibições
- Última mensagem por LuizAquino

Qui Abr 19, 2012 11:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 =
= ![\left[{\left(senx \right)}^{3} \right] - \left[{\left(cosx \right)}^{7} \right] \left[{\left(senx \right)}^{3} \right] - \left[{\left(cosx \right)}^{7} \right]](/latexrender/pictures/4da6df81b35355fd2435511458c74605.png) =
=


 =
= ![\left[{\left(senx \right)}^{3} \right] - \left[{\left(cosx \right)}^{7} \right] \left[{\left(senx \right)}^{3} \right] - \left[{\left(cosx \right)}^{7} \right]](/latexrender/pictures/4da6df81b35355fd2435511458c74605.png) =
=