 é diferenciável em
é diferenciável em  , expresse o valor deste limite em função de
, expresse o valor deste limite em função de 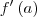 :
: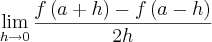
Fazendo a substituição
 , então
, então  :
:Portanto,
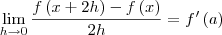
Aqui considero que o limite dado pela questão pode ser escrito em função de
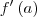 , pois se considerar primeiramente os seguintes limites isoladamente:
, pois se considerar primeiramente os seguintes limites isoladamente: 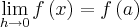
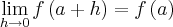
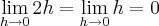
Assim o limite dado pela questão:
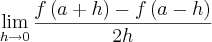 , pode ser reescrito como
, pode ser reescrito como 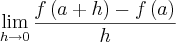
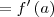 , pois cada limite de cada termo do limite da questão considerado isoladamente resulta no mesmo valor do limite que depois considerados juntamente resulta em
, pois cada limite de cada termo do limite da questão considerado isoladamente resulta no mesmo valor do limite que depois considerados juntamente resulta em 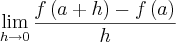
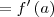
Alguém tem outra explicação?


 .
.  ser diferenciável no ponto
ser diferenciável no ponto  implica
implica 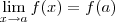 ,além disso
,além disso  (para algum
(para algum  real ).Assim ,
real ).Assim ,  .
.  que é uma função contínua em toda a reta .
que é uma função contínua em toda a reta .  .
.

 .
.
 :
: