 por netochaves » Qui Abr 04, 2013 18:04
por netochaves » Qui Abr 04, 2013 18:04
Uma caixa d’agua no formato de um cilindro circular reto de raio r e altura h será construída em cima de um prédio onde o teto tem formato de um cone de revolução com raio R e altura H, conforme a figura abaixo.
A figura é um cilindro circular reto inscrito num cone reto. Onde o r e o h são o raio e a altura do cilindro e o R e H o raio e altura do cone.
Colocando valores como exemplo para a formula : R vale 5 m, e H vale 12 m.
encontrar as dimensões de r (em função de R e H) que maximiza a área total da superfície da caixa d’ água (inclusive a base inferior).
Questões:
Tem como solucionar a situação sem a aplicação das derivadas?
Qual as dimensões de r (em função de R e H) que maximiza a área total da superfície da caixa d’ água (inclusive a base inferior)?
Qual a solução gráfica para a questao?
-
netochaves
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qui Abr 04, 2013 17:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por young_jedi » Qui Abr 04, 2013 20:02
por young_jedi » Qui Abr 04, 2013 20:02
utilizando semelhanças de triangulos temos que
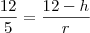
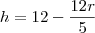
então agora vamos calcular a area superficial do cilindro
a area lateral sera
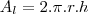
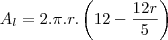
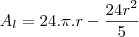
a area da base superior e inferior sera

sendo assim a area total sera


esta é a função de uma parabola com a concavidade voltada para baixo portanto seu valor maximo esta no vertice da parabola, tente proseguir apartir daqui
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Russman » Qui Abr 04, 2013 20:53
por Russman » Qui Abr 04, 2013 20:53
Amigo
young_jedi, acredito que você tenha se confundido na obtenção da área lateral como função de

. Você esqueceu de levar o
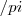
com a fração.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por young_jedi » Qui Abr 04, 2013 21:10
por young_jedi » Qui Abr 04, 2013 21:10
é verdade, foi erro de digitação tem um \pi multiplicadno

portanto a area total é

valeu ai Russman
Editado pela última vez por
young_jedi em Sex Abr 05, 2013 15:14, em um total de 1 vez.
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por netochaves » Sex Abr 05, 2013 14:54
por netochaves » Sex Abr 05, 2013 14:54
Mas gostaria de saber como ficaria a resolução sem adotar valores para R e H, como ficaria as equações ?
-
netochaves
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qui Abr 04, 2013 17:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por young_jedi » Sex Abr 05, 2013 15:24
por young_jedi » Sex Abr 05, 2013 15:24
é so colocar as constante R e H no lugar dos numeros
utilizando semelhanças de triangulos temos que


então agora vamos calcular a area superficial do cilindro
a area lateral sera
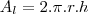
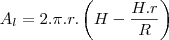
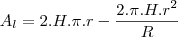
a area da base superior e inferior sera

sendo assim a area total sera
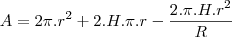
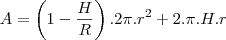
esta é a função de uma parabola com a concavidade voltada para baixo portanto seu valor maximo esta no vertice da parabola, tente proseguir apartir daqui
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por netochaves » Sex Abr 05, 2013 17:41
por netochaves » Sex Abr 05, 2013 17:41
Muito obrigado, agora gostaria de saber como ficaria usando a derivada da função, e o gráfico ficará mesmo uma parábola voltada para baixo né?
-
netochaves
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qui Abr 04, 2013 17:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por young_jedi » Sex Abr 05, 2013 18:10
por young_jedi » Sex Abr 05, 2013 18:10
utilizando a derivada
é so pegar essa expressão da area e derivar com relação a r e igular a 0
o grafico é sim uma parabola, mais o fato dela ser para cima ou para baixo, vai depender dos valores de R e H
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por netochaves » Qua Mai 01, 2013 04:59
por netochaves » Qua Mai 01, 2013 04:59
Mas a questao nao esta pedindo pra colocar r (em funcao de R e H) ?
ou seja essa equacao h= H-H.r/R nao teria que isolar o r, em vez de h?
-
netochaves
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qui Abr 04, 2013 17:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por young_jedi » Qua Mai 01, 2013 11:24
por young_jedi » Qua Mai 01, 2013 11:24
o exercicio pede para encontrar o valor de que maximize o valor da area sendo este calculado em função de H e R
como voce tem a função da area A em função do raio r sendo esta uma parabola, voce tem que o valor maximo de area sera no vertice da parabola então temos que

então o r no vertice da parabola sera


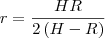
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por netochaves » Qua Mai 01, 2013 16:31
por netochaves » Qua Mai 01, 2013 16:31
ah tah, é o X d vertice né? Xv= -b/2a
é essa mesma a resposta, agora gostaria de saber as situacoes quando :
se H<2R, se H=2R e H>2R , só falta isso para terminar
-
netochaves
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Qui Abr 04, 2013 17:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Cilindro Circular Reto Inscrito em Cone
 por OtavioBonassi » Ter Jul 12, 2011 18:29
por OtavioBonassi » Ter Jul 12, 2011 18:29
- 1 Respostas
- 4271 Exibições
- Última mensagem por Adriano Tavares

Dom Jan 01, 2012 17:51
Geometria Espacial
-
- ME AJUDE POR FAVOR:Cilindro circular reto inscrito no cone
por netochaves » Sex Abr 05, 2013 14:32
- 0 Respostas
- 1827 Exibições
- Última mensagem por netochaves

Sex Abr 05, 2013 14:32
Cálculo: Limites, Derivadas e Integrais
-
- [Volume de um cilindro circular reto]
por liahxs » Dom Ago 13, 2017 23:34
- 0 Respostas
- 4935 Exibições
- Última mensagem por liahxs

Dom Ago 13, 2017 23:34
Geometria Espacial
-
- Volume - Cone circular reto
 por deividchou » Ter Ago 18, 2015 15:57
por deividchou » Ter Ago 18, 2015 15:57
- 2 Respostas
- 5101 Exibições
- Última mensagem por deividchou

Qua Ago 19, 2015 10:31
Geometria Espacial
-
- Dimensões de um cilindro circular
por leticiapires52 » Qua Nov 25, 2015 16:01
- 1 Respostas
- 4407 Exibições
- Última mensagem por adauto martins

Qui Nov 26, 2015 11:18
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


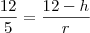
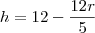
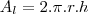
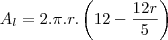
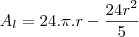




 . Você esqueceu de levar o
. Você esqueceu de levar o 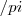 com a fração.
com a fração.



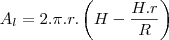
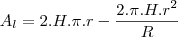
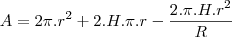
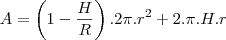



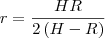


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.