 por Jefferson_mcz » Sex Mar 29, 2013 19:28
por Jefferson_mcz » Sex Mar 29, 2013 19:28
Usando as definições de limites e continuidade como mostrar que a função é continua no intervalo dado ??
G(x) =
![2 \frac{}{}\sqrt[]{3-x} 2 \frac{}{}\sqrt[]{3-x}](/latexrender/pictures/95aa9e191c6b2b3b947d9afe7ec52368.png)
, (-?,3]
F(x) =

, (2,?)
-
Jefferson_mcz
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sáb Mar 16, 2013 11:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por e8group » Sex Mar 29, 2013 21:34
por e8group » Sex Mar 29, 2013 21:34
Uma função é contínua se ,e somente se , elá é contínua em todo ponto de seu domínio . Dica : tome as funções ,
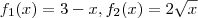
e defina
![f(x) = f_2 (f_1(x)) , D_{f} = D_{f_1} \cap Im_{f_2} = (-\infty , 3] f(x) = f_2 (f_1(x)) , D_{f} = D_{f_1} \cap Im_{f_2} = (-\infty , 3]](/latexrender/pictures/822821ea9e55be3c25fbfaddf0cbbb9e.png)
. Mostre que se

e

forem contínuas ,

também o é .
Tente concluir ...
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Jefferson_mcz » Sex Mar 29, 2013 21:49
por Jefferson_mcz » Sex Mar 29, 2013 21:49
Certo, mais oq não entendo é: Pra uma Função ser continua num dado intervalo ela tem que ser continua em seus pontos do intervalo, então lim x->a tem que ser igual a f(a) certo ? dai no primeiro caso faço fazer o Lim x->-? e o Lim x-> 3, dai se ambos valores foram iguais a f(-?) e f(3) a função é continua, mais f(-?) não existe então como a função é continua no intervalo ? ja no segundo caso faço o mesmo Lim x-> 2 e Lim x->? e se forem iguais a f(2) e f(?) então é continua, sendo que o Lim x->2 é igual a f(2) blz, mais e o lim x->?, que nesse caso não existe então como a função é continua no intervalo dado ? e em relação ao intervalo ser aberto ou fechado tem algum problema ?
-
Jefferson_mcz
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sáb Mar 16, 2013 11:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por e8group » Sex Mar 29, 2013 22:04
por e8group » Sex Mar 29, 2013 22:04
Para mostra que

é contínua temos que impor que para todo

,
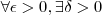
(correspondente de

) tal que torne verdadeira a seguinte afirmação :
"

" ...
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limites] Ajuda com limites no infinito e continuidade
 por umbrorz » Dom Abr 15, 2012 00:54
por umbrorz » Dom Abr 15, 2012 00:54
- 3 Respostas
- 4774 Exibições
- Última mensagem por umbrorz

Seg Abr 16, 2012 11:46
Cálculo: Limites, Derivadas e Integrais
-
- Continuidade/Limites
 por joaofonseca » Sáb Dez 03, 2011 19:40
por joaofonseca » Sáb Dez 03, 2011 19:40
- 3 Respostas
- 2145 Exibições
- Última mensagem por LuizAquino

Sáb Dez 03, 2011 21:27
Cálculo: Limites, Derivadas e Integrais
-
- Limites e continuidade
por Marcos_Mecatronica » Sáb Abr 27, 2013 19:38
- 2 Respostas
- 1725 Exibições
- Última mensagem por e8group

Dom Abr 28, 2013 21:32
Cálculo: Limites, Derivadas e Integrais
-
- Limites(Continuidade)
 por brunotorres123-abc » Sáb Mar 21, 2015 19:35
por brunotorres123-abc » Sáb Mar 21, 2015 19:35
- 0 Respostas
- 1751 Exibições
- Última mensagem por brunotorres123-abc

Sáb Mar 21, 2015 19:35
Cálculo: Limites, Derivadas e Integrais
-
- Limites e Continuidade
por elisafrombrazil » Qui Jan 19, 2017 11:11
- 3 Respostas
- 5438 Exibições
- Última mensagem por adauto martins

Sex Jan 20, 2017 16:24
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![2 \frac{}{}\sqrt[]{3-x} 2 \frac{}{}\sqrt[]{3-x}](/latexrender/pictures/95aa9e191c6b2b3b947d9afe7ec52368.png) , (-?,3]
, (-?,3] , (2,?)
, (2,?)
![2 \frac{}{}\sqrt[]{3-x} 2 \frac{}{}\sqrt[]{3-x}](/latexrender/pictures/95aa9e191c6b2b3b947d9afe7ec52368.png) , (-?,3]
, (-?,3] , (2,?)
, (2,?)
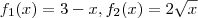 e defina
e defina ![f(x) = f_2 (f_1(x)) , D_{f} = D_{f_1} \cap Im_{f_2} = (-\infty , 3] f(x) = f_2 (f_1(x)) , D_{f} = D_{f_1} \cap Im_{f_2} = (-\infty , 3]](/latexrender/pictures/822821ea9e55be3c25fbfaddf0cbbb9e.png) . Mostre que se
. Mostre que se  e
e  forem contínuas ,
forem contínuas ,  também o é .
também o é .

 é contínua temos que impor que para todo
é contínua temos que impor que para todo  ,
, 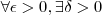 (correspondente de
(correspondente de  ) tal que torne verdadeira a seguinte afirmação :
) tal que torne verdadeira a seguinte afirmação :  " ...
" ...