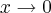 .
.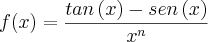 (onde
(onde  é uma constante positiva.)
é uma constante positiva.)(Considere 3 casos:
 é menor ou igual a 2,
é menor ou igual a 2,  é igual a 3,
é igual a 3,  é maior ou igual a 4.)
é maior ou igual a 4.)Sei que para resolver tenho que eliminar o caso do denominador se aproximar de zero, mas como eliminar um fator em
 quando o numerador está em função da tangente e o seno de x?
quando o numerador está em função da tangente e o seno de x?Tipo o resultado é um valor finito, pois o numerador e o denominador representam a razão
 , quando
, quando 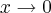 e por isso mesmo o numerador e o denominador podem possuir fatores comuns, usando também o seguinte limite:
e por isso mesmo o numerador e o denominador podem possuir fatores comuns, usando também o seguinte limite: 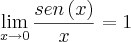 .
.

 .
.  , ou seja ,se
, ou seja ,se  podemos multiplicar
podemos multiplicar  por
por 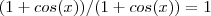 obtendo uma outra função,
obtendo uma outra função,  .
. temos que
temos que  e
e  ;logo
;logo 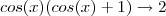 .
. 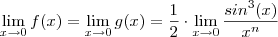 .
. 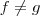 , mas ambas funções possuem o mesmo limite quando
, mas ambas funções possuem o mesmo limite quando 
 e
e  , ou seja
, ou seja  quando x tende a zero ser igual a 1, para fatorar a expressão, mas resulta em:
quando x tende a zero ser igual a 1, para fatorar a expressão, mas resulta em: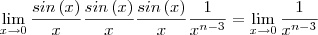
 .
. sempre
sempre 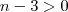 .Para concluir ,estude ambos limites laterais .
.Para concluir ,estude ambos limites laterais .
 .
.
 :
: