 por Douglas16 » Qui Mar 28, 2013 13:35
por Douglas16 » Qui Mar 28, 2013 13:35
Calcule o limite da seguinte função quando
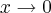
.
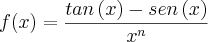
(onde

é uma constante positiva.)
(Considere 3 casos:

é menor ou igual a 2,

é igual a 3,

é maior ou igual a 4.)
Sei que para resolver tenho que eliminar o caso do denominador se aproximar de zero, mas como eliminar um fator em

quando o numerador está em função da tangente e o seno de x?
Tipo o resultado é um valor finito, pois o numerador e o denominador representam a razão

, quando
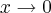
e por isso mesmo o numerador e o denominador podem possuir fatores comuns, usando também o seguinte limite:
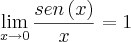
.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Qui Mar 28, 2013 15:00
por e8group » Qui Mar 28, 2013 15:00
Note que :

.
E ainda ,se

, ou seja ,se

podemos multiplicar

por
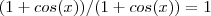
obtendo uma outra função,

.
Quando

temos que

e

;logo
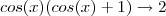
.
Assim ,
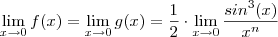
.
OBS.:
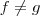
, mas ambas funções possuem o mesmo limite quando

Tente concluir .
Editado ...
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Douglas16 » Sex Mar 29, 2013 11:10
por Douglas16 » Sex Mar 29, 2013 11:10
Mas ainda continua com a indeterminação pois

e

, ou seja

, posso também usar o fato de que o limite de

quando x tende a zero ser igual a 1, para fatorar a expressão, mas resulta em:
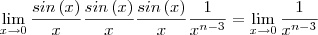
Que no caso quando:
1. n é menor ou igual a 2, o limite é igual a zero.
2. n é igual a 3, o limite é igual a

.
3. n é maior ou igual a 4, o limite é o igual a zero.
Seria isso a solução?
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Sex Mar 29, 2013 12:00
por e8group » Sex Mar 29, 2013 12:00
Em todos os casos exceto o 3 sua resposta está certa .Observe que no caso 3 , para todo

sempre
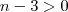
.Para concluir ,estude ambos limites laterais .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Douglas16 » Sex Mar 29, 2013 12:08
por Douglas16 » Sex Mar 29, 2013 12:08
Aqui foi um descuido, o limite no caso 3 é o infinito positivo pelo lado esquerdo e infinito negativo pelo lado direito, ou seja não existe limite.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Onde esta o meu erro
por VERTAO » Dom Mar 13, 2011 20:37
- 1 Respostas
- 2695 Exibições
- Última mensagem por Rogerio Murcila

Qua Mar 16, 2011 23:11
Matemática Financeira
-
- [Integral por partes] onde está o erro???
por Fabio Wanderley » Seg Mai 28, 2012 20:21
- 2 Respostas
- 2474 Exibições
- Última mensagem por Fabio Wanderley

Ter Mai 29, 2012 13:42
Cálculo: Limites, Derivadas e Integrais
-
- Expressões, onde esta o erro que eu não achei
por teilom » Sáb Ago 11, 2012 20:37
- 2 Respostas
- 3568 Exibições
- Última mensagem por teilom

Dom Ago 12, 2012 12:32
Equações
-
- [Estudo do sinal] dessa função. Onde está o erro?
por marcosmuscul » Ter Mar 19, 2013 15:56
- 3 Respostas
- 2931 Exibições
- Última mensagem por marcosmuscul

Sex Mar 22, 2013 00:14
Álgebra Elementar
-
- [Integral Definida] Ex. do tipo "onde está o erro?"
por Fabio Wanderley » Seg Out 22, 2012 23:15
- 2 Respostas
- 2832 Exibições
- Última mensagem por Fabio Wanderley

Ter Out 23, 2012 00:24
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
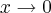 .
.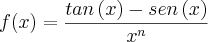 (onde
(onde  é uma constante positiva.)
é uma constante positiva.) é menor ou igual a 2,
é menor ou igual a 2,  é igual a 3,
é igual a 3,  é maior ou igual a 4.)
é maior ou igual a 4.) quando o numerador está em função da tangente e o seno de x?
quando o numerador está em função da tangente e o seno de x? , quando
, quando 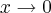 e por isso mesmo o numerador e o denominador podem possuir fatores comuns, usando também o seguinte limite:
e por isso mesmo o numerador e o denominador podem possuir fatores comuns, usando também o seguinte limite: 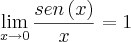 .
.

 .
.  , ou seja ,se
, ou seja ,se  podemos multiplicar
podemos multiplicar  por
por 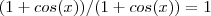 obtendo uma outra função,
obtendo uma outra função,  .
. temos que
temos que  e
e  ;logo
;logo 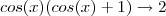 .
. 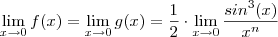 .
.  , mas ambas funções possuem o mesmo limite quando
, mas ambas funções possuem o mesmo limite quando 
 e
e  , ou seja
, ou seja  quando x tende a zero ser igual a 1, para fatorar a expressão, mas resulta em:
quando x tende a zero ser igual a 1, para fatorar a expressão, mas resulta em: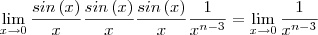
 .
. sempre
sempre 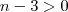 .Para concluir ,estude ambos limites laterais .
.Para concluir ,estude ambos limites laterais .
 .
.



