
Como
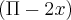 e
e 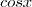 tendem a zero quando
tendem a zero quando  , então o limite existe.
, então o limite existe.Agora só não sei se devo anular
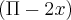 com
com 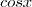 , para eliminar a indeterminação ou devo procurar uma identidade para resolver o limite.
, para eliminar a indeterminação ou devo procurar uma identidade para resolver o limite.

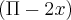 e
e 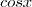 tendem a zero quando
tendem a zero quando  , então o limite existe.
, então o limite existe.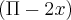 com
com 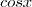 , para eliminar a indeterminação ou devo procurar uma identidade para resolver o limite.
, para eliminar a indeterminação ou devo procurar uma identidade para resolver o limite.
 .
.  segue ,
segue , .
. 
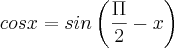 .
.
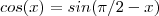 .De fato ,
.De fato , 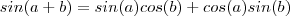 confirma isto ,onde
confirma isto ,onde 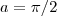 e
e  .
.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 .
.
 :
: