 por Douglas16 » Sáb Mar 16, 2013 21:52
por Douglas16 » Sáb Mar 16, 2013 21:52

Como
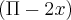
e
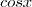
tendem a zero quando

, então o limite existe.
Agora só não sei se devo anular
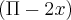
com
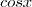
, para eliminar a indeterminação ou devo procurar uma identidade para resolver o limite.
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Sáb Mar 16, 2013 23:39
por e8group » Sáb Mar 16, 2013 23:39
Note que ,

.
De

segue ,

.
Consegue concluir ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Douglas16 » Dom Mar 17, 2013 00:07
por Douglas16 » Dom Mar 17, 2013 00:07
Eu tinha conseguido resolver antes de verificar se alguém tinha respondido, mas entendi sua resolução, e considerei mais simples que a minha resolução, bastava apenas lembrar da propriedade de que
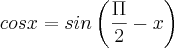
.
Tipo, eu me impressiono comigo mesmo pela falta de capacidade de lembrar de coisas óbvias, vou tentar me concertar e vê o que está acontecendo comigo.
O que você faz para encontrar a resolução tão facilmente, tipo, você não esquece dessas propriedades?
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
 por e8group » Dom Mar 17, 2013 00:34
por e8group » Dom Mar 17, 2013 00:34
Apenas deduzo ,não consigo lembrar muitas coisas .Do ponto de vista geométrico é fácil ver que
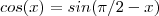
.De fato ,
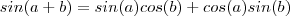
confirma isto ,onde
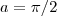
e

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Limite] função trigonométrica
por rafaelbr91 » Ter Mar 27, 2012 17:51
- 2 Respostas
- 2162 Exibições
- Última mensagem por rafaelbr91

Ter Mar 27, 2012 18:43
Cálculo: Limites, Derivadas e Integrais
-
- Limite de uma função trigonométrica
por Douglas16 » Seg Mar 11, 2013 14:45
- 1 Respostas
- 1387 Exibições
- Última mensagem por Douglas16

Seg Mar 11, 2013 15:32
Cálculo: Limites, Derivadas e Integrais
-
- Limite de função trigonométrica
por Carolminera » Qui Jul 17, 2014 15:44
- 4 Respostas
- 2987 Exibições
- Última mensagem por Carolminera

Dom Jul 20, 2014 21:52
Cálculo: Limites, Derivadas e Integrais
-
- Limite de função trigonométrica
por Fernandobertolaccini » Qua Jul 30, 2014 23:27
- 1 Respostas
- 2692 Exibições
- Última mensagem por Man Utd

Qui Ago 07, 2014 15:37
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda com limite de função trigonométrica
por sofa » Qua Jun 29, 2011 04:42
- 6 Respostas
- 3608 Exibições
- Última mensagem por sofa

Qua Jun 29, 2011 06:25
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

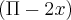 e
e 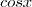 tendem a zero quando
tendem a zero quando  , então o limite existe.
, então o limite existe.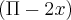 com
com 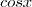 , para eliminar a indeterminação ou devo procurar uma identidade para resolver o limite.
, para eliminar a indeterminação ou devo procurar uma identidade para resolver o limite.

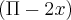 e
e 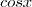 tendem a zero quando
tendem a zero quando  , então o limite existe.
, então o limite existe.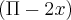 com
com 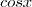 , para eliminar a indeterminação ou devo procurar uma identidade para resolver o limite.
, para eliminar a indeterminação ou devo procurar uma identidade para resolver o limite.
 .
.  segue ,
segue , .
. 
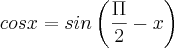 .
.
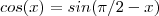 .De fato ,
.De fato , 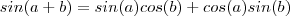 confirma isto ,onde
confirma isto ,onde 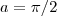 e
e  .
.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
