 por vinit » Ter Mar 12, 2013 12:26
por vinit » Ter Mar 12, 2013 12:26
-
vinit
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Mar 12, 2013 12:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por Douglas16 » Ter Mar 12, 2013 14:40
por Douglas16 » Ter Mar 12, 2013 14:40
Existe uma forma específica de determinar se um limite existe em função fracionária que é:
Em geral em uma função fracionária f(x)/g(x), se limite de f(x) é diferente de zero e limite de g(x) é igual a zero não existe um valor limite (finito).
Mas se limite de f(x) é igual a zero e limite de g(x) também é igual a zero então existe um valor limite (finito).
Então note que na função dada por você tanto o numerador quanto o denominador possuem valores diferentes de zero quando substituo o valor de r por infinito, mas também não dá um valor que se possa determinar com precisão, por isso divida cada termo do numerador e do denominador por x³, ou seja a variável de maior grau, perceba o que acontece com cada termo agora, quando x se aproxima do infinito, tipo: 1/x, por exemplo, se aproxima de zero, entende?, então considere como zero, e depois de considerar o que acontece com cada termo, você obterá um valor para o numerador e o denominador, então basta simplificar dividindo o numerador pelo denominador.
Se Deus quiser, posso passar mais exercícios especialmente para aprender sobre limites via skype, pois se for através de escrita fica muito pesado para mim.
Vai postando suas dúvidas...
-
Douglas16
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Seg Fev 11, 2013 19:15
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- como resolvo isso
por weverton » Dom Jul 18, 2010 23:56
- 1 Respostas
- 1587 Exibições
- Última mensagem por MarceloFantini

Seg Jul 19, 2010 03:18
Estatística
-
- [Sequência] Como resolvo esse Limite
por locatelli » Sex Jan 25, 2013 12:10
- 1 Respostas
- 1895 Exibições
- Última mensagem por young_jedi

Sáb Jan 26, 2013 11:56
Sequências
-
- E agora? Dúvida em limites
por Cleyson007 » Sáb Jun 09, 2012 16:24
- 3 Respostas
- 2284 Exibições
- Última mensagem por MarceloFantini

Dom Jun 10, 2012 15:30
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo] Como estudar ?
por Pessoa Estranha » Sáb Nov 02, 2013 17:54
- 0 Respostas
- 2096 Exibições
- Última mensagem por Pessoa Estranha

Sáb Nov 02, 2013 17:54
Cálculo: Limites, Derivadas e Integrais
-
- Exercícios de Estatística. como estudar ou o que.
por RichardMath » Qui Jun 14, 2018 10:34
- 0 Respostas
- 12712 Exibições
- Última mensagem por RichardMath

Qui Jun 14, 2018 10:34
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
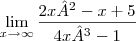






 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.