[LIMITES] Limites Trigonométricos

[felipeek]

Olá,

Apenas sabendo o limite fundamental:



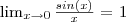
e sem utilizar L'Hopital é possível calcular qualquer limite trigonométrico?

Pergunto isso pois todo livro/aula de cálculo sempre recorre ao limite fundamental na hora de ensinar Limites Trigonométricos e todos exercícios são sempre baseados nesse limite especial.

Então fica a pergunta: Esse limite é tão poderoso assim a ponto de sempre conseguir resolver qualquer problema ou os livros sempre colocam ênfase nesse limite pelo fato dele ser muito importante para achar a derivada de sin(x) e cos(x)?

Obrigado

[Russman]

É verdade que esse resultado é amplamente aplicável, mas não sejamos radicais...

[felipeek]

hehe, é que na verdade o que se busca é um "método" para resolver qualquer problema similiar. Só não consigo me sentir confortável tentando reduzir tudo ao limite fundamental quando resolvo limites de trigonometria. Parece que aqueles exercícios foram "feitos" pra poderem ser resolvidos daquela maneira, entende? Claro que com L'Hopital torna-se muito mais fácil de resolver qualquer lim trigonométrico, mas mesmo assim os métodos de resolução "braçais" não parecem muito confiáveis