 por manuoliveira » Qua Fev 27, 2013 18:55
por manuoliveira » Qua Fev 27, 2013 18:55
Dois lados de um triângulo têm comprimentos a = 4cm e b = 3cm, mas estão crescendo a uma taxa de 1 cm/s. Se a área do triângulo permanece constante, a qual taxa está variando o ângulo alfa entre a e b quando alfa = pi/6.
Agradeço desde já quem puder ajudar!
-
manuoliveira
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qui Abr 01, 2010 19:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
 por Russman » Qua Fev 27, 2013 20:15
por Russman » Qua Fev 27, 2013 20:15
Primeiramente, você deve estabelecer a relação entre a área do triângulo, seus lados conhecidos e o angulo entre eles. Existe a fórmula

onde

é a área,

e

os lados conhecidos e

o ângulo entre eles.
Diferenciando a fórmula com relação a

, obtemos
![\frac{\mathrm{d} S}{\mathrm{d} t} = \frac{1}{2}\frac{\mathrm{d} }{\mathrm{d} t}\left ( ab\sin \left ( \alpha \right ) \right ) = \frac{1}{2}\left [ \frac{\mathrm{d} (ab)}{\mathrm{d} t}\sin \left ( \alpha \right )+\cos \left ( \alpha \right ).\frac{\mathrm{d}\alpha }{\mathrm{d} t}ab \right ] \frac{\mathrm{d} S}{\mathrm{d} t} = \frac{1}{2}\frac{\mathrm{d} }{\mathrm{d} t}\left ( ab\sin \left ( \alpha \right ) \right ) = \frac{1}{2}\left [ \frac{\mathrm{d} (ab)}{\mathrm{d} t}\sin \left ( \alpha \right )+\cos \left ( \alpha \right ).\frac{\mathrm{d}\alpha }{\mathrm{d} t}ab \right ]](/latexrender/pictures/b2f0e27d38bc3f13123066341ed9de5a.png)
.
Como a área é constante, temos
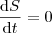
. Isolando, então, a taxa de variação de

aplicando a regra
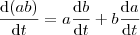
obtemos, finalmente
![\frac{\mathrm{d} \alpha }{\mathrm{d} t} = -\tan \left ( \alpha \right )\left [ \frac{1}{b}\frac{\mathrm{d} b}{\mathrm{d} t}+\frac{1}{a}\frac{\mathrm{d} a}{\mathrm{d} t} \right ] \frac{\mathrm{d} \alpha }{\mathrm{d} t} = -\tan \left ( \alpha \right )\left [ \frac{1}{b}\frac{\mathrm{d} b}{\mathrm{d} t}+\frac{1}{a}\frac{\mathrm{d} a}{\mathrm{d} t} \right ]](/latexrender/pictures/6df2f19f4d950eab8c1bc78b67930516.png)
Agora, substitua os valores dos lados, das taxas de crescimento e o valor do angulo que você obterá a taxa de variação desse angulo. (:
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por manuoliveira » Qui Fev 28, 2013 09:04
por manuoliveira » Qui Fev 28, 2013 09:04
Obrigada!!!
-
manuoliveira
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qui Abr 01, 2010 19:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Taxa de variação
por felipe_ad » Ter Jun 29, 2010 19:44
- 2 Respostas
- 60623 Exibições
- Última mensagem por Guill

Ter Fev 21, 2012 21:17
Cálculo: Limites, Derivadas e Integrais
-
- Taxa de variação
 por AlbertoAM » Sáb Mai 21, 2011 14:23
por AlbertoAM » Sáb Mai 21, 2011 14:23
- 1 Respostas
- 5498 Exibições
- Última mensagem por LuizAquino

Dom Mai 22, 2011 13:03
Cálculo: Limites, Derivadas e Integrais
-
- Taxa de Variação
 por AlbertoAM » Sáb Mai 28, 2011 15:53
por AlbertoAM » Sáb Mai 28, 2011 15:53
- 10 Respostas
- 10660 Exibições
- Última mensagem por AlbertoAM

Ter Mai 31, 2011 21:32
Cálculo: Limites, Derivadas e Integrais
-
- Taxa de Variação
 por Pollyanna Moraes » Sáb Out 22, 2011 17:37
por Pollyanna Moraes » Sáb Out 22, 2011 17:37
- 1 Respostas
- 8471 Exibições
- Última mensagem por LuizAquino

Dom Out 23, 2011 10:15
Cálculo: Limites, Derivadas e Integrais
-
- taxa de variacao
por cal12 » Dom Nov 27, 2011 16:46
- 3 Respostas
- 5411 Exibições
- Última mensagem por Russman

Sex Jun 29, 2012 22:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 é a área,
é a área,  e
e  os lados conhecidos e
os lados conhecidos e  o ângulo entre eles.
o ângulo entre eles. , obtemos
, obtemos![\frac{\mathrm{d} S}{\mathrm{d} t} = \frac{1}{2}\frac{\mathrm{d} }{\mathrm{d} t}\left ( ab\sin \left ( \alpha \right ) \right ) = \frac{1}{2}\left [ \frac{\mathrm{d} (ab)}{\mathrm{d} t}\sin \left ( \alpha \right )+\cos \left ( \alpha \right ).\frac{\mathrm{d}\alpha }{\mathrm{d} t}ab \right ] \frac{\mathrm{d} S}{\mathrm{d} t} = \frac{1}{2}\frac{\mathrm{d} }{\mathrm{d} t}\left ( ab\sin \left ( \alpha \right ) \right ) = \frac{1}{2}\left [ \frac{\mathrm{d} (ab)}{\mathrm{d} t}\sin \left ( \alpha \right )+\cos \left ( \alpha \right ).\frac{\mathrm{d}\alpha }{\mathrm{d} t}ab \right ]](/latexrender/pictures/b2f0e27d38bc3f13123066341ed9de5a.png) .
.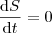 . Isolando, então, a taxa de variação de
. Isolando, então, a taxa de variação de 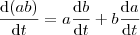 obtemos, finalmente
obtemos, finalmente![\frac{\mathrm{d} \alpha }{\mathrm{d} t} = -\tan \left ( \alpha \right )\left [ \frac{1}{b}\frac{\mathrm{d} b}{\mathrm{d} t}+\frac{1}{a}\frac{\mathrm{d} a}{\mathrm{d} t} \right ] \frac{\mathrm{d} \alpha }{\mathrm{d} t} = -\tan \left ( \alpha \right )\left [ \frac{1}{b}\frac{\mathrm{d} b}{\mathrm{d} t}+\frac{1}{a}\frac{\mathrm{d} a}{\mathrm{d} t} \right ]](/latexrender/pictures/6df2f19f4d950eab8c1bc78b67930516.png)


 .
.



