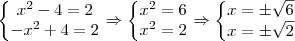e
e 
e preciso determinar a área da região limitada simultaneamente pelas curvas das duas funções
esbocei o gráfico http://www.wolframalpha.com/input/?i=y%3D|x%C2%B2-4|%3B+y%3D2
a partir dai eu pesquisei um pouco pois não me lembrava como descobrir onde as retas se tocavam fazendo
 deu
deu ![x=\sqrt[]{3} x=\sqrt[]{3}](/latexrender/pictures/523b5ee3434676b965de6142a602f32d.png) e o segundo ponto
e o segundo ponto
então pesquisei 1 pouco mais e vi que para descobrir a área das duas funções era só fazer
![A=\int_{\sqrt[]{3}}^{3}f(x) - \int_{\sqrt[]{3}}^{3}g(x) A=\int_{\sqrt[]{3}}^{3}f(x) - \int_{\sqrt[]{3}}^{3}g(x)](/latexrender/pictures/abe8d7966e539f2b602391145a49b561.png)
Calculos:

![\int_{\sqrt[]{3}}^{3}|{x}^{2}-4| dx = \int_{\sqrt[]{3}}^{3}|{x}^{2}-4| dx =](/latexrender/pictures/e412dd1ef60eae7419795ac2d206422a.png)
![{x}^{3}/3 - 4x\int_{\sqrt[]{3}}^{3} = {x}^{3}/3 - 4x\int_{\sqrt[]{3}}^{3} =](/latexrender/pictures/df23a7264bb2cbf43a19ee3b358bc621.png)
![{3}^{3}/3 - 4*3-({\sqrt[]{3})^{3}/3 - 4*\sqrt[]{3}) = {3}^{3}/3 - 4*3-({\sqrt[]{3})^{3}/3 - 4*\sqrt[]{3}) =](/latexrender/pictures/3479521adaf56dc257b86d368b481bee.png)
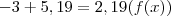

![\int_{\sqrt[]{3}}^{3}2 dx = \int_{\sqrt[]{3}}^{3}2 dx =](/latexrender/pictures/879f8985dad8863b25eb2a3bbf9da463.png)
![2x\int_{\sqrt[]{3}}^{3} = 2x\int_{\sqrt[]{3}}^{3} =](/latexrender/pictures/ebd850547122d61407fd5bc8c78b2b97.png)
![2*3-2 \sqrt[]{3}= 2*3-2 \sqrt[]{3}=](/latexrender/pictures/019e6c441bcd348126ea7938eeb3927b.png)

e cheguei no resultado

Alguem poderia me dizer se o que eu fiz esta certo, errado? obrg


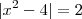

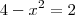

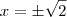


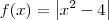 e
e  . A 2° função é a Função Constante que não há nenhum detalhe a se preocupar. Já a 1° função temos um módulo envolvido, de forma que teremos de definí-la por partes. Lembre-se que
. A 2° função é a Função Constante que não há nenhum detalhe a se preocupar. Já a 1° função temos um módulo envolvido, de forma que teremos de definí-la por partes. Lembre-se que

 e
e 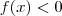 .
.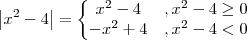
![\left | x^2-4 \right |=\left\{\begin{matrix}
x^2-4 &,-2 \geq x\geq 2 \\
-x^2 + 4 &, 2> x > -2
\end{matrix}\right. = \left\{\begin{matrix}
x^2-4 &,(-\infty ,-2]\cup [2,\infty ) \\
-x^2 + 4 &, (-2,2)
\end{matrix}\right. \left | x^2-4 \right |=\left\{\begin{matrix}
x^2-4 &,-2 \geq x\geq 2 \\
-x^2 + 4 &, 2> x > -2
\end{matrix}\right. = \left\{\begin{matrix}
x^2-4 &,(-\infty ,-2]\cup [2,\infty ) \\
-x^2 + 4 &, (-2,2)
\end{matrix}\right.](/latexrender/pictures/df9731e660f2591b52871cfe9eed3904.png)