Bom vamos a duvida...existem dois limites que estou tendo dificuldades de resolver, principalmente em começar!
Este é o primeiro: Penso eu que poderia fazer pelo metodo do fog: lim f(g(x)), tentei..mais nao deu certo!
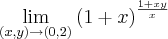
Este é o segundo: Tentei racionaliza-lo, só que ainda ano poderia substituir os valores, pois o denominador iria zerar!
![\lim_{(x,y)\rightarrow(1,1)}\frac{\sqrt[3]{xy}-1}{\sqrt[2]{xy}-1} \lim_{(x,y)\rightarrow(1,1)}\frac{\sqrt[3]{xy}-1}{\sqrt[2]{xy}-1}](/latexrender/pictures/e52beca78d7db3174492162f0133f2eb.png)
Desde ja, agradeço!


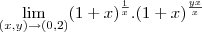
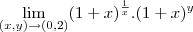
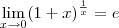
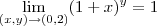
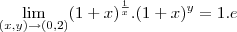

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)