 m, determine o comprimento mínimo de arame necessário para a armação.
m, determine o comprimento mínimo de arame necessário para a armação. 
Como estou fazendo: x = PC (C é o ponto no topo da caixinha da figura). Então DC = 4 - x (PD é a reta que corta o triângulo em dois lados iguais).
Por pitágoras: AP = BP =
![\sqrt[]{3+(4-x)^2} \sqrt[]{3+(4-x)^2}](/latexrender/pictures/b95aee7a046cf5c6025b2c9e38561810.png)
O comprimento do arame é: AP + BP + PC.
Então tenho a função comprimento:
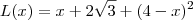
Derivei essa função aí pela regra da cadeia e obtive:
![L'(x) = 1 + \frac{2x-8}{(\sqrt[]{x^2-8x+19})} L'(x) = 1 + \frac{2x-8}{(\sqrt[]{x^2-8x+19})}](/latexrender/pictures/964e29a5ef97fae57ef4a764708ec1d5.png)
Tentei achar os pontos críticos, mas acho que me perdi a partir daí, pois da forma que prossigo não bate o gabarito. Como devo prosseguir? Desde já grato.


 .
. tomemos
tomemos  e
e 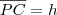 , de forma que
, de forma que .
.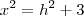 , de forma que
, de forma que  .
.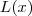 que é dada por
que é dada por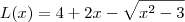 .
. o qual
o qual 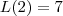 .
.

 .
.



