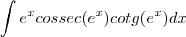
bom, chamei de u=e^x , logo, du= e^xdx
que após alguns ajustes, me resultou em :
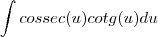
só que após isso eu não consigo resolver...
eu teria que colocar tudo em função de senos e cossenos?
eu tentei assim, porém me resultou numa integral assim:
aí chamei v=sin(u) , logo dv= cos(u)du
mas aí ficou:
mas a integral da cossec² (u) é -cotg(u) , o que não bate com a resposta do livro, que é -cossec(e^x) + c
![\\ \int \frac{1}{v^2} \, dv = \\\\\\ \int v^{- 2 } \, dv = \\\\\\ \left[ v^{- 1} \cdot - 1 \right] = \\\\ \left[ \frac{- 1}{v} \right] = \\\\\\ \left[ \frac{- 1}{sen \, u} \right] = \\\\\\ \left[ \frac{- 1}{sen \, \left(e^x \right)} \right] = \\\\\\ \boxed{ - cossec \, \left(e^x \right) + c}](/latexrender/pictures/66745e0cfef04c42432f810097a22ada.png "\\ \int \frac{1}{v^2} \, dv = \\\\\\ \int v^{- 2 } \, dv = \\\\\\ \left[ v^{- 1} \cdot - 1 \right] = \\\\ \left[ \frac{- 1}{v} \right] = \\\\\\ \left[ \frac{- 1}{sen \, u} \right] = \\\\\\ \left[ \frac{- 1}{sen \, \left(e^x \right)} \right] = \\\\\\ \boxed{ - cossec \, \left(e^x \right) + c}")
.
: