 por rodrigonapoleao » Qui Dez 27, 2012 16:59
por rodrigonapoleao » Qui Dez 27, 2012 16:59

dividindo os polinomios fico com
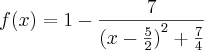
como faço para primitivar a função?
-
rodrigonapoleao
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Nov 19, 2012 14:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
 por e8group » Qui Dez 27, 2012 18:53
por e8group » Qui Dez 27, 2012 18:53
Basta fazer
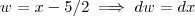
.
Assim ,

.
Agora deixando
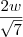
por

,vamos ter
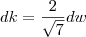
.
Prossegue-se que ,
![-4 \int\frac{dw}{\left( \frac{2w}{\sqrt{7}}\right )^2+1} = - 7 \cdot \int \frac{dw}{w^2+7/4}= -4 \int \frac{dw}{\frac{4w^2}{7}+1} = -4 \int\frac{dw}{\left( \frac{2w}{\sqrt{7}}\right )^2+1} \\ \\
-4 \int\frac{dw}{\left( \frac{2w}{\sqrt{7}}\right )^2+1} = -4 \int\frac{\frac{\sqrt{7}}{2}}{k^2+1}dk = -2\sqrt{7}\int \frac{dk}{k^2+1} = -2\sqrt{7} arctan(k) + c = -2\sqrt{7} arctan\left(\frac{2w}{\sqrt{7}} \right )+c = -2\sqrt{7} arctan\left(\frac{2\left[\frac{2x-5}{2} \right ]}{\sqrt{7}} \right )+c = - 2\sqrt{7} arctan\left(\frac{2x-5}{\sqrt{7}} \right )+c -4 \int\frac{dw}{\left( \frac{2w}{\sqrt{7}}\right )^2+1} = - 7 \cdot \int \frac{dw}{w^2+7/4}= -4 \int \frac{dw}{\frac{4w^2}{7}+1} = -4 \int\frac{dw}{\left( \frac{2w}{\sqrt{7}}\right )^2+1} \\ \\
-4 \int\frac{dw}{\left( \frac{2w}{\sqrt{7}}\right )^2+1} = -4 \int\frac{\frac{\sqrt{7}}{2}}{k^2+1}dk = -2\sqrt{7}\int \frac{dk}{k^2+1} = -2\sqrt{7} arctan(k) + c = -2\sqrt{7} arctan\left(\frac{2w}{\sqrt{7}} \right )+c = -2\sqrt{7} arctan\left(\frac{2\left[\frac{2x-5}{2} \right ]}{\sqrt{7}} \right )+c = - 2\sqrt{7} arctan\left(\frac{2x-5}{\sqrt{7}} \right )+c](/latexrender/pictures/546c414edaf46686d33bd8fa3e1b84dd.png)
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- URGENTE! funções racionais.
por Hugo23 » Dom Mar 13, 2011 13:20
- 6 Respostas
- 4019 Exibições
- Última mensagem por MarceloFantini

Dom Mar 13, 2011 19:04
Funções
-
- Primitivas de funções racionais
por rodrigonapoleao » Seg Dez 17, 2012 14:51
- 1 Respostas
- 1947 Exibições
- Última mensagem por young_jedi

Ter Dez 18, 2012 10:25
Funções
-
- primitivaçao de funçoes racionais
por rodrigonapoleao » Ter Dez 18, 2012 19:16
- 1 Respostas
- 1315 Exibições
- Última mensagem por e8group

Qua Dez 19, 2012 06:33
Cálculo: Limites, Derivadas e Integrais
-
- [Funções Racionais] Contradominio
por sifm » Dom Abr 07, 2013 15:22
- 1 Respostas
- 2234 Exibições
- Última mensagem por young_jedi

Seg Abr 08, 2013 20:44
Funções
-
- Limites no infinito de funções racionais
por Ariane » Ter Out 21, 2008 21:33
- 1 Respostas
- 6619 Exibições
- Última mensagem por Molina

Qua Out 22, 2008 12:23
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 dividindo os polinomios fico com
dividindo os polinomios fico com 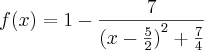

 dividindo os polinomios fico com
dividindo os polinomios fico com 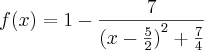

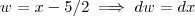 .
.  .
. 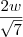 por
por  ,vamos ter
,vamos ter 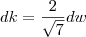 .
. ![-4 \int\frac{dw}{\left( \frac{2w}{\sqrt{7}}\right )^2+1} = - 7 \cdot \int \frac{dw}{w^2+7/4}= -4 \int \frac{dw}{\frac{4w^2}{7}+1} = -4 \int\frac{dw}{\left( \frac{2w}{\sqrt{7}}\right )^2+1} \\ \\
-4 \int\frac{dw}{\left( \frac{2w}{\sqrt{7}}\right )^2+1} = -4 \int\frac{\frac{\sqrt{7}}{2}}{k^2+1}dk = -2\sqrt{7}\int \frac{dk}{k^2+1} = -2\sqrt{7} arctan(k) + c = -2\sqrt{7} arctan\left(\frac{2w}{\sqrt{7}} \right )+c = -2\sqrt{7} arctan\left(\frac{2\left[\frac{2x-5}{2} \right ]}{\sqrt{7}} \right )+c = - 2\sqrt{7} arctan\left(\frac{2x-5}{\sqrt{7}} \right )+c -4 \int\frac{dw}{\left( \frac{2w}{\sqrt{7}}\right )^2+1} = - 7 \cdot \int \frac{dw}{w^2+7/4}= -4 \int \frac{dw}{\frac{4w^2}{7}+1} = -4 \int\frac{dw}{\left( \frac{2w}{\sqrt{7}}\right )^2+1} \\ \\
-4 \int\frac{dw}{\left( \frac{2w}{\sqrt{7}}\right )^2+1} = -4 \int\frac{\frac{\sqrt{7}}{2}}{k^2+1}dk = -2\sqrt{7}\int \frac{dk}{k^2+1} = -2\sqrt{7} arctan(k) + c = -2\sqrt{7} arctan\left(\frac{2w}{\sqrt{7}} \right )+c = -2\sqrt{7} arctan\left(\frac{2\left[\frac{2x-5}{2} \right ]}{\sqrt{7}} \right )+c = - 2\sqrt{7} arctan\left(\frac{2x-5}{\sqrt{7}} \right )+c](/latexrender/pictures/546c414edaf46686d33bd8fa3e1b84dd.png)


 .
.
 :
: