 por MrJuniorFerr » Dom Dez 16, 2012 16:20
por MrJuniorFerr » Dom Dez 16, 2012 16:20
Boa tarde.
Como resolver a seguinte integral:
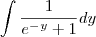
Por partes não dá. Substituição trigonométrica também não. Frações parciais, ao menos por enquanto não. Portanto só me resta o método por substituição.
Tentei o seguinte:
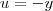
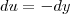
Substituindo, temos:

Aplicando outra substituição:
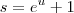

Não há/não sei como fazer aparecer um

no numerador...
O que fazer?
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por MrJuniorFerr » Dom Dez 16, 2012 18:30
por MrJuniorFerr » Dom Dez 16, 2012 18:30
Olá Young_jedi, se eu fizer essa substituição sugerida, eu ainda não vou conseguir resolver a integral, pois sou incapaz de fazer aparecer um

no numerador...
-

MrJuniorFerr
- Colaborador Voluntário

-
- Mensagens: 119
- Registrado em: Qui Set 20, 2012 16:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Alimentos
- Andamento: cursando
 por young_jedi » Dom Dez 16, 2012 18:59
por young_jedi » Dom Dez 16, 2012 18:59
veja o seguinte, chegamos em
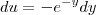
podemos escrever assim
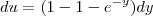
![du=[1-(e^{-y}+1)]dy du=[1-(e^{-y}+1)]dy](/latexrender/pictures/1ed949f422204f2315a49c42ad301779.png)
mais como

então
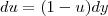
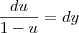
substituindo na integral
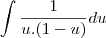
esta integral voce resolve por frações parciais e depois faz a substituição de u
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Quebrando a cabeça ate agora :/
por Amandatkm » Dom Abr 28, 2013 17:48
- 8 Respostas
- 4181 Exibições
- Última mensagem por Amandatkm

Ter Abr 30, 2013 15:03
Equações
-
- [Gráfico de função] Tô quebrando a cabeça
por gu21n » Dom Ago 17, 2014 17:03
- 1 Respostas
- 1337 Exibições
- Última mensagem por Russman

Dom Ago 17, 2014 21:53
Funções
-
- [Integral] Estou com dificuldade para resolver esta integral
por Paulo Perez » Qui Out 03, 2013 12:22
- 2 Respostas
- 4607 Exibições
- Última mensagem por Paulo Perez

Sex Out 04, 2013 16:32
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda para resolver Integral definida
por rodolphogagno » Qua Dez 01, 2010 15:16
- 4 Respostas
- 3575 Exibições
- Última mensagem por Moura

Seg Dez 13, 2010 21:51
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda para resolver equação para calcular velocidade média
por marcorrer » Sex Fev 24, 2012 13:10
- 0 Respostas
- 3701 Exibições
- Última mensagem por marcorrer

Sex Fev 24, 2012 13:10
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
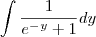
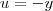


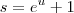

 no numerador...
no numerador... 


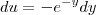
 no numerador...
no numerador...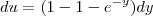
![du=[1-(e^{-y}+1)]dy du=[1-(e^{-y}+1)]dy](/latexrender/pictures/1ed949f422204f2315a49c42ad301779.png)
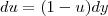
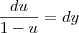
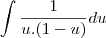
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.