![\lim_{x\to3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3} \lim_{x\to3}\frac{\sqrt[3]{x}-\sqrt[3]{3}}{x-3}](/latexrender/pictures/997ab4ba073e875cf40ba3c42e7f9f12.png)


![(\sqrt[3]{x}-\sqrt[3]{x}) (\sqrt[3]{x}-\sqrt[3]{x})](/latexrender/pictures/2690ff8091b8e64ccd743847b28b4d7b.png) , então desenvolver o numerador, o que encontra?
, então desenvolver o numerador, o que encontra?
 . Então
. Então 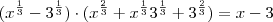 , que poderá ser simplificado com o denominador.
, que poderá ser simplificado com o denominador.

fraol escreveu:Bom dia,
Você já tentou multiplicar tanto o numerador quanto o denominador por, então desenvolver o numerador, o que encontra?
.
![(\sqrt[3]{x}-\sqrt[3]{x}) = 0 (\sqrt[3]{x}-\sqrt[3]{x}) = 0](/latexrender/pictures/e5a2707d09d3ac152e2baa2e50644f87.png) sempre, certo?
sempre, certo?



![\sqrt[3]{x} - \sqrt[3]{x} \sqrt[3]{x} - \sqrt[3]{x}](/latexrender/pictures/35e90c0586a42dcf8b094cde568d769c.png) é a função identicamente nula, pois ela é zero em todos os pontos. Novamente, você está essencialmente multiplicando tudo por zero e dizendo que o resultado é zero. Ora, por esse raciocínio então o limite
é a função identicamente nula, pois ela é zero em todos os pontos. Novamente, você está essencialmente multiplicando tudo por zero e dizendo que o resultado é zero. Ora, por esse raciocínio então o limite  é zero, pois multiplicando e dividindo
é zero, pois multiplicando e dividindo  teremos que o limite é zero.
teremos que o limite é zero.


![\sqrt[3]{x} - \sqrt[3]{3} \sqrt[3]{x} - \sqrt[3]{3}](/latexrender/pictures/0788f790cf907f8c7b649e43062460f1.png) no numerador.
no numerador.
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)