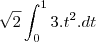por ricardosanto » Qui Dez 06, 2012 04:54
por ricardosanto » Qui Dez 06, 2012 04:54
A massa do fio retilíneo que liga a origem em O e um ponto A= (1,1) e densidade dada por; f(x,y)= 3xy.
minha resposta:
como a reta parte da origem, temos que, O = (0,0) e portanto a variação do x é de 0 até 1.
coomo o x e o y são sempre iguais, eu tirei que a função é y=x.
a fórmula a ser usade é:
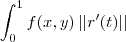
vamos aos cálculos
como o y= x temos que o vetor posição é
r(t) xi+xj(obs. se puder explicar melhor como encontro o vetor posição, eu fico muito grato.)
Agora o vetor tangente:
r'(t)= 1i + 0j
a norma de r'(t)=
![||r'(t)|| = \sqrt[]{ {(1i)}^{2} + {(0j)}^{2} } ||r'(t)|| = \sqrt[]{ {(1i)}^{2} + {(0j)}^{2} }](/latexrender/pictures/e476fdd05df5c7c01ea3d83cf7419532.png)
=
1agora vou substituir y=x na densidade, obtendo: 3xx = 3x²
calculando a integral:

![\frac{3}{3} \left[{x}^{3} \right] \frac{3}{3} \left[{x}^{3} \right]](/latexrender/pictures/dd4024288e61c68b5b1f0e27c4e46710.png)
1*1³=1 <==Resposta.
Obrigado pela atenção.
-
ricardosanto
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Seg Abr 16, 2012 12:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia civil
- Andamento: cursando
 por young_jedi » Sex Dez 07, 2012 12:54
por young_jedi » Sex Dez 07, 2012 12:54
amigo confesso que tambem não entendi muito bem a resolução

esta parte esta parte eu entendi e concordo com isto
mais note que se r é a reta em que x=y
então podemos dizer que x=y=t portanto

portanto

então a integral ficaria

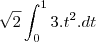
resolvendo

-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Recipiente metálico
por cristina » Sex Nov 12, 2010 09:06
- 4 Respostas
- 3209 Exibições
- Última mensagem por cristina

Qua Nov 17, 2010 10:47
Geometria Espacial
-
- massa?
por Anderson POntes » Sáb Jul 10, 2010 16:46
- 2 Respostas
- 1902 Exibições
- Última mensagem por Anderson POntes

Sáb Jul 10, 2010 17:09
Geometria Plana
-
- Centro da massa
por belabela18 » Dom Set 23, 2018 04:33
- 0 Respostas
- 8502 Exibições
- Última mensagem por belabela18

Dom Set 23, 2018 04:33
Cálculo: Limites, Derivadas e Integrais
-
- Centro de Massa.
 por AnaCarolina22 » Qua Abr 24, 2019 12:45
por AnaCarolina22 » Qua Abr 24, 2019 12:45
- 0 Respostas
- 13338 Exibições
- Última mensagem por AnaCarolina22

Qua Abr 24, 2019 12:45
Mecânica
-
- [Física] Centro de massa
 por renan_a » Sex Out 26, 2012 09:55
por renan_a » Sex Out 26, 2012 09:55
- 1 Respostas
- 2556 Exibições
- Última mensagem por young_jedi

Sex Out 26, 2012 12:15
Fundamentos de Mecânica
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
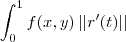
![||r'(t)|| = \sqrt[]{ {(1i)}^{2} + {(0j)}^{2} } ||r'(t)|| = \sqrt[]{ {(1i)}^{2} + {(0j)}^{2} }](/latexrender/pictures/e476fdd05df5c7c01ea3d83cf7419532.png) = 1
= 1
![\frac{3}{3} \left[{x}^{3} \right] \frac{3}{3} \left[{x}^{3} \right]](/latexrender/pictures/dd4024288e61c68b5b1f0e27c4e46710.png)