 por Sobreira » Dom Dez 02, 2012 14:17
por Sobreira » Dom Dez 02, 2012 14:17
Pessoal tenho uma dúvida:

Sei que não é uma função composta então não aplico regra da cadeia.
Mas como faço pra resolver esta derivada???
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por DanielFerreira » Dom Dez 02, 2012 18:40
por DanielFerreira » Dom Dez 02, 2012 18:40
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por MarceloFantini » Seg Dez 03, 2012 00:08
por MarceloFantini » Seg Dez 03, 2012 00:08
Como o Danjr apontou, é uma regra da cadeia sim. Não é uma função elementar.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12552 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14792 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Achar a derivada de uma função
por caiofisico » Seg Set 05, 2011 20:18
- 4 Respostas
- 3839 Exibições
- Última mensagem por caiofisico

Ter Set 06, 2011 19:44
Cálculo: Limites, Derivadas e Integrais
-
- ]Derivada de uma função] derivada com raiz
por Leandro_Araujo » Ter Mar 06, 2012 01:11
- 5 Respostas
- 8550 Exibições
- Última mensagem por LuizAquino

Ter Mar 06, 2012 13:40
Cálculo: Limites, Derivadas e Integrais
-
- derivada de uma função
por jmario » Sex Mai 07, 2010 13:51
- 4 Respostas
- 3795 Exibições
- Última mensagem por Elcioschin

Sex Mai 07, 2010 23:15
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




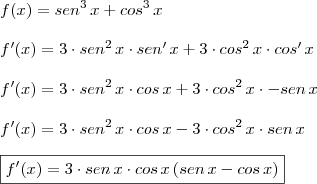



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.