 por Sherminator » Sex Nov 16, 2012 13:13
por Sherminator » Sex Nov 16, 2012 13:13
Boa tarde, alguém me ajuda a resolver este problema?

-
Sherminator
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Out 20, 2012 09:50
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Gestão de Empresas
- Andamento: cursando
 por MarceloFantini » Sex Nov 16, 2012 13:38
por MarceloFantini » Sex Nov 16, 2012 13:38
Sherminator, use figuras apenas se estritamente necessário. Utilize LaTeX para redigir suas equações. Seu tópico não deverá ser respondido até estar de acordo com as regras.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sherminator » Sex Nov 16, 2012 14:18
por Sherminator » Sex Nov 16, 2012 14:18
Peço desculpa, sou novo aqui, já estive a tentar mas acho super complicado, qualquer das formas vou tentar.
-
Sherminator
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Out 20, 2012 09:50
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Gestão de Empresas
- Andamento: cursando
 por MarceloFantini » Sex Nov 16, 2012 14:21
por MarceloFantini » Sex Nov 16, 2012 14:21
Tente, arrumamos o código se necessário.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sherminator » Sex Nov 16, 2012 14:40
por Sherminator » Sex Nov 16, 2012 14:40
![g(x) = \frac{{x}^{3}-8}{\sqrt[]{2x+5}} , se , x>2 g(x) = \frac{{x}^{3}-8}{\sqrt[]{2x+5}} , se , x>2](/latexrender/pictures/f54701dda903beabda8de0cd489c8881.png)
Para a primeira só está a faltar o 3- antes da raiz quadrada que não estou a conseguir
-
Sherminator
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Out 20, 2012 09:50
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Gestão de Empresas
- Andamento: cursando
 por MarceloFantini » Sex Nov 16, 2012 15:01
por MarceloFantini » Sex Nov 16, 2012 15:01
Quase lá. O código é
- Código: Selecionar todos
g(x) = \begin{cases}
\frac{x^3 -8}{3 - \sqrt{2x+5}}, & \text{ se } x >2 \\
|x-8|, & \text{ se } x \leq 2.
\end{cases}
que dá

Agora: qual é a questão? Você só colocou a função e "para x=2".
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sherminator » Sex Nov 16, 2012 15:07
por Sherminator » Sex Nov 16, 2012 15:07
Obrigado

valeu, para a próxima tento fazer melhor
A questão é para estudar a continuidade da função g no ponto indicado. Como posso resolver?
-
Sherminator
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Out 20, 2012 09:50
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Gestão de Empresas
- Andamento: cursando
 por MarceloFantini » Sex Nov 16, 2012 16:48
por MarceloFantini » Sex Nov 16, 2012 16:48
Calcule
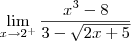
e veja se o resultado é 6, que é o valor da função em

. Este valor foi obtido usando a regra da função, que está definida como

para

, portanto
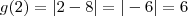
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sherminator » Sáb Nov 17, 2012 08:53
por Sherminator » Sáb Nov 17, 2012 08:53
Não estou a entender muito bem, a função de cima dá zero, verdade? E a de baixo dá 6, nesse caso não é contínua, correto? Devido aos limites laterais não serem iguais é isso?
Terei de resolver a indeterminação da de cima?
-
Sherminator
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Out 20, 2012 09:50
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Gestão de Empresas
- Andamento: cursando
 por MarceloFantini » Sáb Nov 17, 2012 09:04
por MarceloFantini » Sáb Nov 17, 2012 09:04
Segundo o
Wolfram o limite é -36. Como o resultado é diferente do valor da função, não é contínua.

Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sherminator » Sáb Nov 17, 2012 09:10
por Sherminator » Sáb Nov 17, 2012 09:10
Pode-me deixar aqui a resolução completa de como chego ao -36 se faz favor? É que não estou conseguindo.
-
Sherminator
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Out 20, 2012 09:50
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Gestão de Empresas
- Andamento: cursando
 por Sherminator » Dom Nov 18, 2012 16:31
por Sherminator » Dom Nov 18, 2012 16:31
Alguém me dá uma ajudinha a resolver a indeterminação se faz favor?
-
Sherminator
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Out 20, 2012 09:50
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Gestão de Empresas
- Andamento: cursando
 por MarceloFantini » Dom Nov 18, 2012 23:31
por MarceloFantini » Dom Nov 18, 2012 23:31
Ainda não tive tempo de fazer a conta por extenso, por isso usei o Wolfram. Quando conseguir posto.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MarceloFantini » Ter Nov 20, 2012 10:40
por MarceloFantini » Ter Nov 20, 2012 10:40
Apenas corrigi algumas coisas:
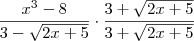
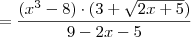

.
Note que na última passagem você encontra o denominador

, por isso dá negativo.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sherminator » Ter Nov 20, 2012 12:55
por Sherminator » Ter Nov 20, 2012 12:55
Obrigado, ainda demoro bastante tempo a postar as funções, por isso dou alguns erros

No denominador descuidei-me com o sinal, mas já vi o erro

-
Sherminator
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Out 20, 2012 09:50
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Gestão de Empresas
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Continuidade de função
por marinalcd » Qui Ago 23, 2012 20:52
- 0 Respostas
- 1045 Exibições
- Última mensagem por marinalcd

Qui Ago 23, 2012 20:52
Funções
-
- Continuidade da função
por Lenin » Qua Set 25, 2013 21:21
- 1 Respostas
- 1368 Exibições
- Última mensagem por Man Utd

Qua Set 25, 2013 21:35
Cálculo: Limites, Derivadas e Integrais
-
- Estudo da [continuidade] de uma função
por Teh_eng » Qui Mai 03, 2012 13:43
- 1 Respostas
- 1372 Exibições
- Última mensagem por Russman

Qui Mai 03, 2012 14:52
Cálculo: Limites, Derivadas e Integrais
-
- [Continuidade de função] Demonstração
por Gustavo Gomes » Qui Nov 08, 2012 21:41
- 2 Respostas
- 1591 Exibições
- Última mensagem por Gustavo Gomes

Sex Nov 09, 2012 21:33
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Continuidade - Função
por raimundoocjr » Ter Mai 07, 2013 20:16
- 1 Respostas
- 1247 Exibições
- Última mensagem por e8group

Ter Mai 07, 2013 21:16
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.









![g(x) = \frac{{x}^{3}-8}{\sqrt[]{2x+5}} , se , x>2 g(x) = \frac{{x}^{3}-8}{\sqrt[]{2x+5}} , se , x>2](/latexrender/pictures/f54701dda903beabda8de0cd489c8881.png)




 valeu, para a próxima tento fazer melhor
valeu, para a próxima tento fazer melhor
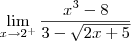 e veja se o resultado é 6, que é o valor da função em
e veja se o resultado é 6, que é o valor da função em  . Este valor foi obtido usando a regra da função, que está definida como
. Este valor foi obtido usando a regra da função, que está definida como  para
para  , portanto
, portanto 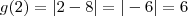 .
.










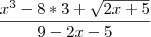


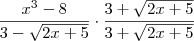
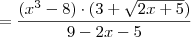
 .
. , por isso dá negativo.
, por isso dá negativo.




![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)