Se um automóvel parte do repouso, qual a aceleração constante que lhe permitirá percorrer 150 metros em 10 segundos?
Não consegui resolver pelo cálculo somente a partir destes dados.
Tentei o seguinte:
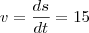 , derivando ambos os lados da igualdade em função de t:
, derivando ambos os lados da igualdade em função de t:
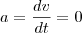 , como podem ver, não deu certo da forma q tentei resolver...
, como podem ver, não deu certo da forma q tentei resolver...Tentei resolver também pela física, mas meu resultado deu:
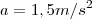 , sendo que de acordo com o gabarito, deveria dar
, sendo que de acordo com o gabarito, deveria dar 
Alguém pode me ajudar?


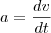
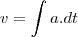
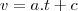


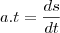
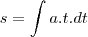

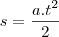
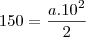


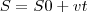



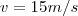

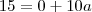



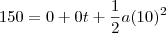


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)