 por Lucas Monteiro » Ter Nov 06, 2012 21:27
por Lucas Monteiro » Ter Nov 06, 2012 21:27
-
Lucas Monteiro
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Jun 25, 2012 18:40
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Ter Nov 06, 2012 22:40
por e8group » Ter Nov 06, 2012 22:40
Note que ,
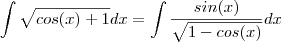
Fazendo
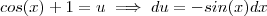
.Assim, segue que :
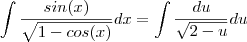
Fazendo uma nova substituição ,
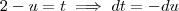
Teremos ,

Voltando para u e depois para x
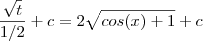
Daí ,
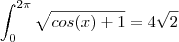
Pergunte aí qualquer coisa .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Lucas Monteiro » Ter Nov 06, 2012 23:30
por Lucas Monteiro » Ter Nov 06, 2012 23:30
![\int_{}^{}\sqrt[]{cos(x) +1}dx=\int_{}^{}\frac{sin(x)}{\sqrt[]{1-cos(x)}}dx \int_{}^{}\sqrt[]{cos(x) +1}dx=\int_{}^{}\frac{sin(x)}{\sqrt[]{1-cos(x)}}dx](/latexrender/pictures/00d373775e0b3fd7b6826a6bfa36010d.png)
Como você fez essa passagem?
-
Lucas Monteiro
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Seg Jun 25, 2012 18:40
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qua Nov 07, 2012 00:02
por e8group » Qua Nov 07, 2012 00:02
Sim , claro .

.
Mas !
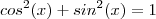
.
Daí ,

OBS.: Desculpe , cometi alguns erros , não adquiri um bom conhecimento sobre integrais ainda . Vou deixar para os demais usuários do ajuda matemática te ajudar . Entretanto vou analisar o mesmo novamente .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Qua Nov 07, 2012 02:01
por MarceloFantini » Qua Nov 07, 2012 02:01
É quase isso. Multiplicando por
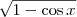
no numerador e denominador, você terá

sobre
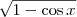
. Ora, mas pela relação fundamental temos
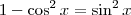
, daí

. Ou seja, agora você precisa quebrar a integral nos intervalos
![[0, \pi] [0, \pi]](/latexrender/pictures/f74f8710fd31ce502365bc814a7fd3b6.png)
e
![[\pi, 2 \pi] [\pi, 2 \pi]](/latexrender/pictures/361b499ec6c385d9f8d8f279e29a208f.png)
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por e8group » Qua Nov 07, 2012 21:23
por e8group » Qua Nov 07, 2012 21:23
Obrigado , Marcelo Fantini . Agora eu consegui .
Vamos fazer primeiro uma observação :
![sin(x) \geq 0 ; x \in [ 0 , \pi ] sin(x) \geq 0 ; x \in [ 0 , \pi ]](/latexrender/pictures/f3d4b46bcafcaf09f1d6c9a7dec5affc.png)
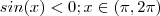
.
Daí ,

e
![| sin(x) | = sin(x) , x \in [ 0 , \pi ] | sin(x) | = sin(x) , x \in [ 0 , \pi ]](/latexrender/pictures/10b0001ce1f830447ed1727e5c079f63.png)
.
Fazendo os procedimentos anteriores do tópico acima , virmos que :

.
De acordo que o Marcelo disse , segue que ;
i)

ii)
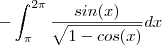
Fazendo ,
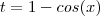
.Donde ,

. Teremos por um lado ,
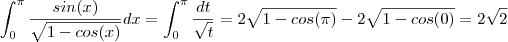
. Entretanto , por outro lado ,

logo ,

.
Se estiver certo , espero que ajude aí .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Boa Tarde Pessoal, Ajuda se puderem!!
por erickeu » Qua Abr 06, 2011 14:19
- 2 Respostas
- 4192 Exibições
- Última mensagem por Kabarosk

Sex Mai 29, 2015 01:34
Mensagens Matemáticas
-
- Números Complexos Ajuda pessoal!
por Reece » Sáb Ago 18, 2012 18:28
- 1 Respostas
- 4923 Exibições
- Última mensagem por MarceloFantini

Sáb Ago 18, 2012 19:23
Números Complexos
-
- ME AJUDEM URGENTE PESSOAL
por Claudia Sotero » Seg Nov 23, 2009 22:15
- 1 Respostas
- 3401 Exibições
- Última mensagem por Neperiano

Sex Set 23, 2011 19:29
Funções
-
- [SEI N ] Pessoal Me ajudem Por favor!
por GarotoBurro » Sáb Mai 12, 2012 23:57
- 1 Respostas
- 1450 Exibições
- Última mensagem por DanielFerreira

Sáb Mai 19, 2012 10:29
Trigonometria
-
- Estou com dúvida pessoal!
por zenildo » Ter Jan 13, 2015 13:53
- 0 Respostas
- 1228 Exibições
- Última mensagem por zenildo

Ter Jan 13, 2015 13:53
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{0}^{2\pi}\sqrt[]{1+cos(x)}dx \int_{0}^{2\pi}\sqrt[]{1+cos(x)}dx](/latexrender/pictures/dfcb67eccacb78184d13813bf60fc60f.png)



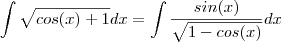
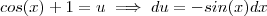 .Assim, segue que :
.Assim, segue que : 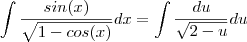
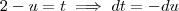

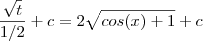
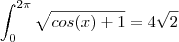

![\int_{}^{}\sqrt[]{cos(x) +1}dx=\int_{}^{}\frac{sin(x)}{\sqrt[]{1-cos(x)}}dx \int_{}^{}\sqrt[]{cos(x) +1}dx=\int_{}^{}\frac{sin(x)}{\sqrt[]{1-cos(x)}}dx](/latexrender/pictures/00d373775e0b3fd7b6826a6bfa36010d.png)

 .
. 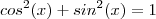 .
. 

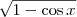 no numerador e denominador, você terá
no numerador e denominador, você terá  sobre
sobre 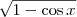 . Ora, mas pela relação fundamental temos
. Ora, mas pela relação fundamental temos 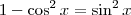 , daí
, daí  . Ou seja, agora você precisa quebrar a integral nos intervalos
. Ou seja, agora você precisa quebrar a integral nos intervalos ![[0, \pi] [0, \pi]](/latexrender/pictures/f74f8710fd31ce502365bc814a7fd3b6.png) e
e ![[\pi, 2 \pi] [\pi, 2 \pi]](/latexrender/pictures/361b499ec6c385d9f8d8f279e29a208f.png) .
.

![sin(x) \geq 0 ; x \in [ 0 , \pi ] sin(x) \geq 0 ; x \in [ 0 , \pi ]](/latexrender/pictures/f3d4b46bcafcaf09f1d6c9a7dec5affc.png)
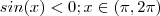 .
.  e
e ![| sin(x) | = sin(x) , x \in [ 0 , \pi ] | sin(x) | = sin(x) , x \in [ 0 , \pi ]](/latexrender/pictures/10b0001ce1f830447ed1727e5c079f63.png) .
.  .
. 
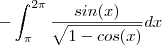
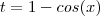 .Donde ,
.Donde ,  . Teremos por um lado ,
. Teremos por um lado ,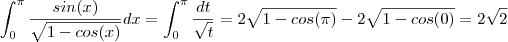 . Entretanto , por outro lado ,
. Entretanto , por outro lado , 
 .
. 
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.