 por fabriel » Seg Out 29, 2012 15:26
por fabriel » Seg Out 29, 2012 15:26
E ai Pessoal então:
é dado essa integral:
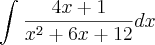
Ai como:
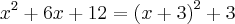
Então:
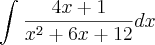
=
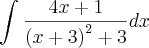
Ai calculando:
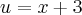
e

Então:
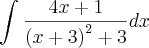
=
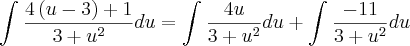
Mas agora estou em duvida pois integrando da um pouco diferente da resposta:
A resposta é:
![2 ln \left({x}^{2}+6x+12 \right)-\frac{11}{\sqrt[]{3}}arc tg\frac{x+3}{\sqrt[]{3}}+c 2 ln \left({x}^{2}+6x+12 \right)-\frac{11}{\sqrt[]{3}}arc tg\frac{x+3}{\sqrt[]{3}}+c](/latexrender/pictures/436e38928dc02ff158279cd65b749d51.png)
Me ajudem nessa questão por favor..Obrigado!
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por young_jedi » Seg Out 29, 2012 17:05
por young_jedi » Seg Out 29, 2012 17:05
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por fabriel » Ter Out 30, 2012 01:48
por fabriel » Ter Out 30, 2012 01:48
Valeu ai young_jedi.
Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Integral] Conferência de resposta
por LAZAROTTI » Dom Set 30, 2012 20:29
- 2 Respostas
- 1907 Exibições
- Última mensagem por MarceloFantini

Seg Out 01, 2012 09:19
Cálculo: Limites, Derivadas e Integrais
-
- Me ajudem pois estou confuso...
por Fiel8 » Sáb Jun 27, 2009 18:41
- 4 Respostas
- 3131 Exibições
- Última mensagem por Fiel8

Sáb Jun 27, 2009 19:20
Funções
-
- dúvida na resposta
por Anderson Claiton 77 » Dom Ago 23, 2015 12:41
- 1 Respostas
- 1360 Exibições
- Última mensagem por Matpas

Qui Ago 27, 2015 17:55
Funções
-
- [limites] dúvida na resposta
por Fabio Wanderley » Dom Nov 11, 2012 23:25
- 2 Respostas
- 1331 Exibições
- Última mensagem por Fabio Wanderley

Dom Nov 25, 2012 11:10
Cálculo: Limites, Derivadas e Integrais
-
- [Limite ao infinito] Dúvida na resposta = 0
por guilherme_vb » Ter Abr 23, 2013 11:27
- 1 Respostas
- 1433 Exibições
- Última mensagem por e8group

Sex Abr 26, 2013 22:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
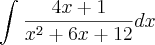
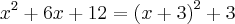
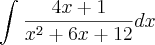 =
= 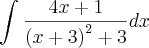
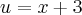 e
e 
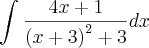 =
=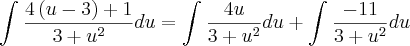
![2 ln \left({x}^{2}+6x+12 \right)-\frac{11}{\sqrt[]{3}}arc tg\frac{x+3}{\sqrt[]{3}}+c 2 ln \left({x}^{2}+6x+12 \right)-\frac{11}{\sqrt[]{3}}arc tg\frac{x+3}{\sqrt[]{3}}+c](/latexrender/pictures/436e38928dc02ff158279cd65b749d51.png)

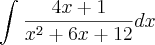
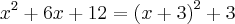
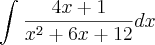 =
= 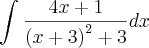
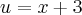 e
e 
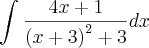 =
=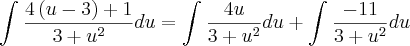
![2 ln \left({x}^{2}+6x+12 \right)-\frac{11}{\sqrt[]{3}}arc tg\frac{x+3}{\sqrt[]{3}}+c 2 ln \left({x}^{2}+6x+12 \right)-\frac{11}{\sqrt[]{3}}arc tg\frac{x+3}{\sqrt[]{3}}+c](/latexrender/pictures/436e38928dc02ff158279cd65b749d51.png)

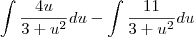
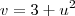
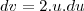
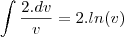
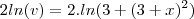

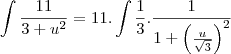
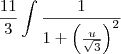
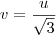
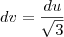
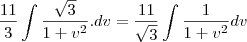
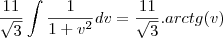
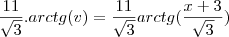
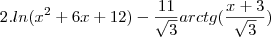


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.