 por Thyago Quimica » Seg Out 29, 2012 18:44
por Thyago Quimica » Seg Out 29, 2012 18:44
Determine o numero real positivo cuja soma com o inverso de seu quadrado seja mínima.
Sei que para poder fazer essa questão é preciso desenvolver a função e a partir dai calcular a derivada e tudo mais...
a minha unica dificuldade e montar a função para dar continuidade a questão, so preciso que alguém monte a função inicial, o resto tou conta.
Quem poder agradeço.
-
Thyago Quimica
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sáb Mai 05, 2012 17:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Química
- Andamento: cursando
 por e8group » Seg Out 29, 2012 19:15
por e8group » Seg Out 29, 2012 19:15
Seja x , este número real . Assim , o mesmo pode ser inverso por

.
Em contexto com enunciado ,teremos a seguinte função
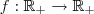
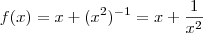
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Aplicações da Derivada
por Bruhh » Qua Jun 02, 2010 19:00
- 2 Respostas
- 4780 Exibições
- Última mensagem por Bruhh

Sáb Jun 05, 2010 18:25
Cálculo: Limites, Derivadas e Integrais
-
- Aplicaçoes lineares (derivada)
por Zanatta » Qua Mai 15, 2013 22:59
- 0 Respostas
- 878 Exibições
- Última mensagem por Zanatta

Qua Mai 15, 2013 22:59
Cálculo: Limites, Derivadas e Integrais
-
- Aplicações de Derivada - Problemas de Otimização - Socorro!!
por Josi » Ter Nov 03, 2009 17:30
- 1 Respostas
- 2799 Exibições
- Última mensagem por marciommuniz

Ter Nov 03, 2009 22:30
Cálculo: Limites, Derivadas e Integrais
-
- Aplicações de Derivada - Problemas de Otimização - Socorro!!
por Josi » Ter Nov 03, 2009 17:31
- 1 Respostas
- 4757 Exibições
- Última mensagem por Elcioschin

Qua Nov 04, 2009 08:40
Cálculo: Limites, Derivadas e Integrais
-
- Aplicações de Derivada [Teorema do valor médio]
por xanda2012 » Sáb Jun 16, 2012 16:22
- 2 Respostas
- 2254 Exibições
- Última mensagem por xanda2012

Sáb Jun 16, 2012 17:43
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 .
. 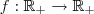
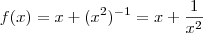 .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)