 por camargo92 » Seg Out 29, 2012 10:10
por camargo92 » Seg Out 29, 2012 10:10
Olá a todos, meu professor passou a seguinte questão e estou com dificuldades para resolver, não consigo montar a resolução do exercício.
"A renda per capita, calculada pela relação entre o PIB (Produto Interno Bruto) e a população, é um indicador de produtividade de um país. Em face da crise por qual passamos, vários foram o órgãos que estimaram um decréscimo do PIB brasileiro em 1999. Entretanto, os fatos demonstraram que houve um pequeno acréscimo estimado em 0,5%. Supondo um crescimento de 1.8% da população do Brasil naquele dado ano, calcular de quanto deverá ser o PIB no próximo ano (2000) para que a renda per capita atinja o mesmo nível de 1998, supondo que a população continue crescendo a uma taxa de 1,8% ao ano."
Agradeço desde já.
-
camargo92
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Out 29, 2012 09:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por young_jedi » Seg Out 29, 2012 12:14
por young_jedi » Seg Out 29, 2012 12:14
a redna per capta de 1998 é igual a
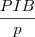
onde p é a população
se a população cresce a taxa de 1,8% ao ano a população de 1999 sera
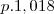
e em 2000 sera
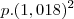
ja o PIB teve um acrescimo de 0,5 % então o PIB em 1999 sera

supondo um acrescimo x no PIB de 1999 para 2000, temos que a renda per capita de 2000 sera dada por
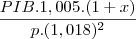
igaulando a de 1998
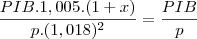
simplificando termos
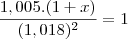
resolvendo encontramos a taxa de crescimento x para 2000 do PIB
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por camargo92 » Seg Out 29, 2012 15:02
por camargo92 » Seg Out 29, 2012 15:02
young_jedi escreveu:a redna per capta de 1998 é igual a
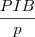
onde p é a população
se a população cresce a taxa de 1,8% ao ano a população de 1999 sera
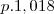
e em 2000 sera
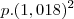
ja o PIB teve um acrescimo de 0,5 % então o PIB em 1999 sera

supondo um acrescimo x no PIB de 1999 para 2000, temos que a renda per capita de 2000 sera dada por
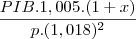
igaulando a de 1998
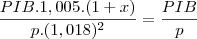
simplificando termos
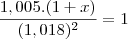
resolvendo encontramos a taxa de crescimento x para 2000 do PIB
muito obrigado! era o que eu precisava.
vlw
-
camargo92
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Out 29, 2012 09:42
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- CRESCIMENTO PERCENTUAL
por patymedeiros54 » Qua Jul 22, 2015 18:30
- 5 Respostas
- 10468 Exibições
- Última mensagem por patymedeiros54

Qui Jul 23, 2015 18:50
Matemática Financeira
-
- Percentual de crescimento sobre zero
por barrufi » Qua Mar 10, 2010 22:21
- 2 Respostas
- 17489 Exibições
- Última mensagem por marcos goncalves

Sáb Dez 08, 2012 12:16
Matemática Financeira
-
- Calculo percentual não da valor exato?
por fabianosilva » Qua Ago 10, 2011 17:07
- 4 Respostas
- 3602 Exibições
- Última mensagem por fabianosilva

Qui Ago 11, 2011 17:28
Álgebra Elementar
-
- Juros e Renda
por Puru Osso » Dom Jun 05, 2011 17:51
- 0 Respostas
- 1262 Exibições
- Última mensagem por Puru Osso

Dom Jun 05, 2011 17:51
Matemática Financeira
-
- Problema sobre renda per capita
por matem » Dom Dez 11, 2011 09:01
- 3 Respostas
- 3746 Exibições
- Última mensagem por Neperiano

Dom Dez 11, 2011 13:07
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


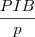
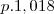
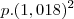

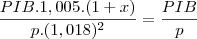
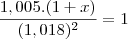

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.