![\lim_{x\to5/3}\sqrt[2]{\left|x \right|+\left|\left|3x \right| \right|+4} \lim_{x\to5/3}\sqrt[2]{\left|x \right|+\left|\left|3x \right| \right|+4}](/latexrender/pictures/2affed0cd64c81fa00bc48d02d1ca32d.png)


![\lim_{x\to5/3}\sqrt[2]{\left|x \right|+\left|\left|3x \right| \right|+4} \lim_{x\to5/3}\sqrt[2]{\left|x \right|+\left|\left|3x \right| \right|+4}](/latexrender/pictures/2affed0cd64c81fa00bc48d02d1ca32d.png)

mih123 escreveu:Olá, estou em dúvida em alguns exercícios de limite com módulo. Tentei fazer este aqui,mas não sei como fazer os dois limites laterais!
 quanto para
quanto para  temos que x e 3x são números positivos. Sendo assim, em ambos os casos teremos |x| = x e |3x| = 3x (e obviamente ||3x|| = |3x| = 3x).
temos que x e 3x são números positivos. Sendo assim, em ambos os casos teremos |x| = x e |3x| = 3x (e obviamente ||3x|| = |3x| = 3x).
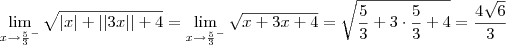

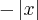 ?? Pensei que nos limites laterais,um seria positivo e o outro negativo.Faço muita confusão com isso.
?? Pensei que nos limites laterais,um seria positivo e o outro negativo.Faço muita confusão com isso.
mih123 escreveu:Eu ainda tenho uma dúvida,quando será?? Pensei que nos limites laterais,um seria positivo e o outro negativo.Faço muita confusão com isso.


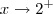 , o número 3x - 6 é positivo. Faça um teste: escolha x = 2,1 e calcule 3x - 6. Dessa forma, como o número 3x - 6 é positivo, temos que |3x - 6| = 3x - 6 e ficamos com:
, o número 3x - 6 é positivo. Faça um teste: escolha x = 2,1 e calcule 3x - 6. Dessa forma, como o número 3x - 6 é positivo, temos que |3x - 6| = 3x - 6 e ficamos com:
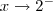 , o número 3x - 6 é negativo. Faça um teste: escolha x = 1,9 e calcule 3x - 6. Dessa forma, como o número 3x - 6 é negativo, temos que |3x - 6| = -(3x - 6) e ficamos com:
, o número 3x - 6 é negativo. Faça um teste: escolha x = 1,9 e calcule 3x - 6. Dessa forma, como o número 3x - 6 é negativo, temos que |3x - 6| = -(3x - 6) e ficamos com:
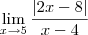
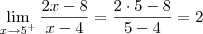



Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.