Prova de que o limite não existe.

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

Prova de que o limite não existe.

Regras do fórum
Responder

Prova de que o limite não existe.

Mensagempor arthur_ » Sáb Ago 22, 2009 21:29

olá, sou arthur, estou cursando meu primeiro período de engenharia na UFPE,
e tem uma questão de limite que nao consigo provar.

\lim_{\ x\to2}\frac{x^2-x+6}{x-2}

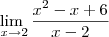
a resposta atrás do livro diz o limite não existe. mas eu queria saber como se prova isso.
obrigado!
arthur_
Novo Usuário
Novo Usuário
 
Mensagens: 2
Registrado em: Sáb Ago 22, 2009 21:17
Formação Escolar: GRADUAÇÃO
Área/Curso: Engenharia
Andamento: cursando
Voltar ao topo

Re: Prova de que o limite não existe.

Mensagempor Felipe Schucman » Dom Ago 23, 2009 14:53

arthur_ escreveu:olá, sou arthur, estou cursando meu primeiro período de engenharia na UFPE,
e tem uma questão de limite que nao consigo provar.

\lim_{\ x\to2}\frac{x^2-x+6}{x-2}

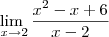
a resposta atrás do livro diz o limite não existe. mas eu queria saber como se prova isso.
obrigado!


É o seguinte Arthur eu começaria tentando provar que o limite pela direita e pela esquerda não é o mesmo, de forma que se relamente não for seu problema esta resolvido....
Felipe Schucman
Usuário Parceiro
Usuário Parceiro
 
Mensagens: 52
Registrado em: Ter Jul 28, 2009 17:39
Formação Escolar: GRADUAÇÃO
Área/Curso: Economia e Direito
Andamento: cursando
Voltar ao topo

Re: Prova de que o limite não existe.

Mensagempor arthur_ » Dom Ago 23, 2009 15:12

que vacilo cara, é mesmo havia me esquecido completamente da unicidade dos limites
você esta certo, o lim da esquerda é diferente do da direita!

obrigado!
arthur_
Novo Usuário
Novo Usuário
 
Mensagens: 2
Registrado em: Sáb Ago 22, 2009 21:17
Formação Escolar: GRADUAÇÃO
Área/Curso: Engenharia
Andamento: cursando
Voltar ao topo
Responder

Voltar para Cálculo: Limites, Derivadas e Integrais

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 


Tópico Popular

Assunto: simplifiquei e achei...está certo?????????????
Autor: zig - Sex Set 23, 2011 13:57

{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}

Assunto: simplifiquei e achei...está certo?????????????
Autor: Vennom - Sex Set 23, 2011 21:41

zig escreveu:{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}


Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo: {\frac{1}{4}}^{-1} = \frac{4}{1}

Então pense o seguinte: a fração geratriz de 0,05 é \frac{1}{20} , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja: {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}

A raiz quadrada de vinte, você acha fácil, né?

Espero ter ajudado.

Assunto: simplifiquei e achei...está certo?????????????
Autor: fraol - Dom Dez 11, 2011 20:23

Nós podemos simplificar, um pouco, sqrt(20) da seguinte forma:

sqrt(20) = sqrt(4 . 5) = sqrt( 2^2 . 5 ) = 2 sqrt(5).

É isso.

Assunto: simplifiquei e achei...está certo?????????????
Autor: fraol - Dom Dez 11, 2011 20:24

Nós podemos simplificar, um pouco, \sqrt(20) da seguinte forma:

\sqrt(20) = \sqrt(4 . 5) = \sqrt( 2^2 . 5 ) = 2 \sqrt(5).

É isso.

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

Índice do fórum