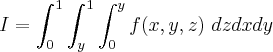
na ordem dx dy dz.

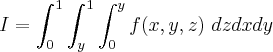

ivoski escreveu: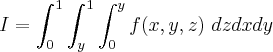
na ordem dx dy dz.
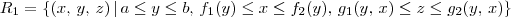
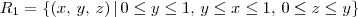
 ,
, 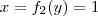 ,
,  e
e 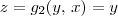 .
.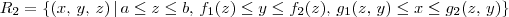
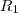 , note que
, note que 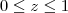 .
.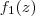 e
e  , precisamos projetar
, precisamos projetar 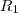 no plano yz. Nesse caso, precisamos projetar no plano yz o triângulo de vértices (1, 0, 0), (1, 1, 0) e (1, 1, 1). Essa projeção será simplesmente o triângulo de vértices (0, 0, 0), (0, 1, 0) e (0, 1, 1). Analisando esses pontos no plano yz, obtemos que
no plano yz. Nesse caso, precisamos projetar no plano yz o triângulo de vértices (1, 0, 0), (1, 1, 0) e (1, 1, 1). Essa projeção será simplesmente o triângulo de vértices (0, 0, 0), (0, 1, 0) e (0, 1, 1). Analisando esses pontos no plano yz, obtemos que 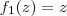 e
e  . Ou seja, temos que
. Ou seja, temos que 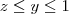 .
. e
e 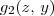 . Analisando
. Analisando 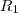 , note que x é delimitado inferiormente pelo plano que passa por (0,0,0), (1,1,0) e (1, 1, 1). A equação desse plano é dada por x - y = 0. Desse modo, temos que
, note que x é delimitado inferiormente pelo plano que passa por (0,0,0), (1,1,0) e (1, 1, 1). A equação desse plano é dada por x - y = 0. Desse modo, temos que 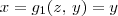 . Por outro lado, perceba que x é delimitado superiormente pelo plano x = 1. Sendo assim, temos que
. Por outro lado, perceba que x é delimitado superiormente pelo plano x = 1. Sendo assim, temos que 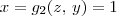 . Ou seja, temos que
. Ou seja, temos que 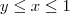 .
.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes





