Estou com dúvidas em relação e expressões dentro de raíz, sei que para tirar um numero x, da raiz tem de eleva-lo a 1/2, mas com uma expressão não sei como que fica.
Por exemplo Derivada de Raiz de( 2T + 3) , ou derivada Raiz de (1-9u²)
Desde já agradeço a atenção recebida



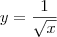
 .
.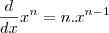 , então
, então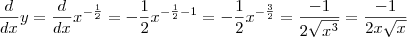 .
.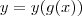 , então
, então .
. . Isto é indicado pela notação "
. Isto é indicado pela notação " " .
" .![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)