Olá pessoal, o professor passou uma lista e só falta uma questão para resolver, é a seguinte:
Faça a mudança de variável necessária e para calcular a seguinte integral:
como não sei ainda usar as ferramentas aqui, vou colocar integral como: "S"
S(de -1 a 1)S(de -raiz(1-x²) a raiz(1-x²)S(x²+y²)² a 1. x²dzdydx
a resposta é pi\8
acho que o problema principal é fazer a mudança de variável, sei que x²+y²= r², então ficaria, de r^4 a 1.
Alguém poderia pelo menos me ajudar a converter utilizando, coordenadas cilíndricas ou esféricas.
Acho que irei conseguir fazer depois de converter.
Ficarei muito grata.


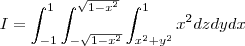 .
.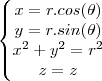


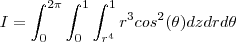 .
.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)