 por samra » Qua Jun 13, 2012 22:03
por samra » Qua Jun 13, 2012 22:03
Olá pessoal, boa noite

Se possível, me ajudem a resolver esta questão, por gentileza:
Verifique a aproximação linear dada em a=0 .
A seguir, determine os valores de x para os quais
a aproximação linear tem precisão de 0,1.a)
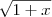

1 +
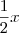
b) tg x

x
c)1/(1+2x)^4

1-8x
d) e^x

1 + x
obs: me ajudem só com a letra
a msm (por favor), só pra eu pegar a idéia, e as demais eu tento fazer sozinha

(a menos qe a idéia para resolver as msm seja diferente)
não soube resolver a parte destacada em sublinhado.Muito Obrigada.
Abraço :*
respostas:
a) -0,69<x<1,09
c)-0,045<x<0,055"sábio é aquele que conhece os limites da própria ignorância" Sócrates
-
samra
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sex Jan 27, 2012 11:31
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Técnico em Informatica
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [aproximação linear]
por Giu » Qua Fev 15, 2012 06:09
- 1 Respostas
- 1473 Exibições
- Última mensagem por LuizAquino

Qua Fev 15, 2012 18:26
Cálculo: Limites, Derivadas e Integrais
-
- Aproximação linear
por joaopaulo_ » Sáb Jun 23, 2012 16:59
- 2 Respostas
- 2740 Exibições
- Última mensagem por joaopaulo_

Dom Jun 24, 2012 11:28
Cálculo: Limites, Derivadas e Integrais
-
- Aproximação Linear
por RonnieAlmeida » Sex Mai 23, 2014 00:18
- 0 Respostas
- 1659 Exibições
- Última mensagem por RonnieAlmeida

Sex Mai 23, 2014 00:18
Cálculo: Limites, Derivadas e Integrais
-
- Aproximação linear
por leandrocalixto » Ter Out 04, 2016 15:33
- 0 Respostas
- 1948 Exibições
- Última mensagem por leandrocalixto

Ter Out 04, 2016 15:33
Cálculo: Limites, Derivadas e Integrais
-
- Aproximação
por Thais Aquino Lima » Qui Fev 28, 2013 19:28
- 1 Respostas
- 1320 Exibições
- Última mensagem por Cleyson007

Sex Mar 01, 2013 09:13
Aritmética
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

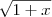
 1 +
1 + 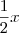
 x
x 1-8x
1-8x 1 + x
1 + x



 .
.



