

O que quer dizer "calcular mais rapidamente"?
Não consegui interpretar isto.
E o que ele quis dizer com Fxy (ou Fyx) qual a diferença?
Se poder, explica como devo prceder.
Desde já obrigado




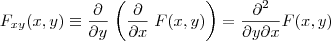 .
.
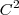 .
.



 quando a função for de classe
quando a função for de classe 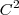 , ou seja, tem derivadas parciais contínuas até segunda ordem. Sabendo que são iguais, pode existir uma ordem que facilite o seu trabalho, e é isto que o exercício pede que você encontre. Note que na primeira temos
, ou seja, tem derivadas parciais contínuas até segunda ordem. Sabendo que são iguais, pode existir uma ordem que facilite o seu trabalho, e é isto que o exercício pede que você encontre. Note que na primeira temos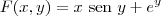 .
. se anula pois quando tratamos de derivadas parciais consideramos as outras constantes. Logo
se anula pois quando tratamos de derivadas parciais consideramos as outras constantes. Logo 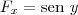 . Agora, derivando em relação a y, segue
. Agora, derivando em relação a y, segue  .
.

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 14 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.